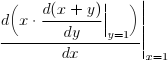(An alternative title for this post is, what is the type of differentiation? Hint: it’s not quite (ℝ→ℝ)→(ℝ→ℝ), because how would you make sure the input function is differentiable?)

You can download this post as a literate Haskell program.

{-# LANGUAGE Rank2Types             #-}
{-# LANGUAGE MultiParamTypeClasses  #-}
{-# LANGUAGE FlexibleInstances      #-}
{-# LANGUAGE FunctionalDependencies #-}
{-# LANGUAGE UndecidableInstances   #-}
{-# LANGUAGE OverlappingInstances   #-}

module Differentiation where

Automatic differentiation

The overloading approach to automatic differentiation has become more popular recently among typed functional programmers. The basic idea is to overload arithmetic operators such as +, ×, and sin so that they work on not just floating-point numbers but pairs (or more generally, sequences) of them, which track quantities along with their rates of change. The overloaded operators are easy to define because, unlike with integration, the rules of differentiation are compositional: you know, d(x + y) = dx + dy, d(x × y) = dx × y + x × dy, d(sin x) = cos x × dx, and so on. Here they are in Haskell.

data D a = D a a
  deriving Show

lift :: Num a => a -> D a
lift x = D x 0

infinitesimal :: Num a => D a
infinitesimal = D 0 1

instance Eq a => Eq (D a) where
  D x _ == D y _ = x == y

instance Ord a => Ord (D a) where
  compare (D x _) (D y _) = compare x y

instance Num a => Num (D a) where
  D x x' + D y y' = D (x + y) (x' + y')
  D x x' * D y y' = D (x * y) (x' * y + x * y')
  negate (D x x') = D (negate x) (negate x')
  abs    (D x x') = D (abs x) (signum x * x')
  signum (D x _)  = lift (signum x)
  fromInteger x   = lift (fromInteger x)

instance Fractional a => Fractional (D a) where
  recip (D x x') = D (recip x) (-x'/x/x)
  fromRational x = lift (fromRational x)

The two components of a D value are a quantity and its derivative, so the lift function ‘lifts’ a number to a constant quantity, and infinitesimal is a quantity with value 0 and derivative 1. Were abs defined by abs x = signum x * x by default, we wouldn’t have to define abs for D above.

Let us use these definitions to model how a parabola reflects light.

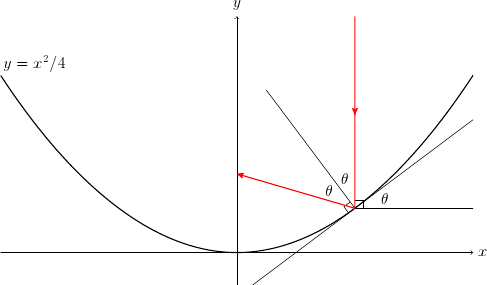
Suppose that a light ray (red above) enters a parabolic mirror y = x²/4 from above. Where does the reflected ray cross the y axis? In the diagram above, if the point where the ray hits the parabola is (x,y), then the derivative of y with respect to x is tan θ, and the y coordinate where the reflected ray crosses the y axis is y + x/tan 2θ, which is equal to y + x (1/tan θ − tan θ)/2. We can compute this coordinate by automatically differentiating y with respect to x:

curve x = x^2/4

reflect x = let D y y' = curve (lift x + infinitesimal)
            in y + x * (recip y' - y') / 2

As expected, the parabola reflects all incoming rays from above to the focal point (0,1).

*Differentiation> map reflect [1..5]
[1.0,1.0,1.0,1.0,1.0]

To be sure, this code does not work by symbolically differentiating y = x²/4 to yield y′ = x/2. Rather, it computes y alongside y′ for one particular x at a time, so the curve could just as well be defined by a more complex program that uses if and recursion. For example, a ray tracer usually deals with scenes much more complex than a single parabola. This code also does not work by numerically comparing the values of y at nearby values of x. Instead of approximating dy/dx by Δy/Δx where Δx is a very small real number, we compute with an actually infinitesimal dx.

Differentiation is a higher-order function

Before we continue, let us abstract the pattern for differentiation in reflect above into a new higher-order function d, which differentiates any given function at the input 0. For convenience, d also returns the value of the given function at 0.

d :: Num a => (D a -> D b) -> (b, b)
d f = let D y y' = f infinitesimal
      in (y,y')

reflect :: Fractional a => a -> a
reflect x = let (y,y') = d (\h -> curve (lift x + h))
            in y + x * (recip y' - y') / 2

Even though the reflect function uses differentiation internally, we can still differentiate it. Such differentiate is said to be nested. For the parabola, we can confirm that the reflected ray hits the focal point not just at but also around x = 3, because the derivative computed below is zero.

*Differentiation> d (\k -> reflect (3 + k))
(1.0,0.0)

For other curves and surfaces, the derivative is typically not zero and tells us the density of light energy that falls around each point on the y axis. Hence, as Dan Piponi noted, this kind of calculation is performed by ray tracers and other programs that sample from probability distributions.

Another application of automatic differentiation is to find roots of a function using Newton’s method. Therefore, we can use nested automatic differentiation to find local extrema and saddle points of a function using Newton’s method.

The danger of confusing infinitesimals

Jeff Siskind and Barak Pearlmutter pointed out a kind of programmer mistake that makes nested differentiation give the wrong result. As they show, this kind of mistake is easy to make in the framework defined above, because all it takes is putting a call to the lift function in the wrong place. The definition of reflectBug below is only slightly different from reflect, but the result is very different and very wrong.

reflectBug x = let (y,y') = d (\h -> lift (curve (x + h)))
               in y + x * (recip y' - y') / 2

*Differentiation> d (\k -> reflectBug (3 + k))
(Infinity,NaN)

They demonstrate this problem using running code in Haskell and Scheme that computes

to be 2 rather than the correct answer 1.

The essence of this problem is that the two nested invocations of differentiation use two different infinitesimals, which a mathematician would denote by dh and dk. These two infinitesimals should not be confused, just as years and feet and persons should not be confused.

Using types to check units

Björn Buckwalter showed that we can use a generic type system to prevent such confusion statically, just as Haskell uses state threads to distinguish pointers into different memory regions. Recall that the type ST s a in Haskell represents a monadic computation that yields a result of type a using mutable cells in the state thread represented by the phantom type s. To construct such a computation, we can use primitive operations such as

newSTRef :: a -> ST s (STRef s a)

and the fact that ST s is a monad. To run such a computation, we must use the primitive function

runST :: (forall s. ST s a) -> a

in which forall s forces different state threads, created by different calls to runST, to be represented by different phantom types s. One way to understand this rank-2 type is that it makes the type checker generate a new phantom type s for each argument to runST. Analogously, Buckwalter redefines the type constructor D to take a phantom-type argument s, which represents an infinitesimal unit.

data D s a = D a a
  deriving Show

Accordingly, the other definitions above change in their types, but not in their terms or behavior. The most important change is the new rank-2 type of d, which forces different infinitesimals, created by different invocations of differentiation, to be represented by different phantom types s.

d :: Num a => (forall s. D s a -> D s a) -> (a, a)
d f = let D y y' = f infinitesimal
      in (y,y')

lift :: Num a => a -> D s a
lift x = D x 0

infinitesimal :: Num a => D s a
infinitesimal = D 0 1

instance Eq a => Eq (D s a) where
  D x _ == D y _ = x == y

instance Ord a => Ord (D s a) where
  compare (D x _) (D y _) = compare x y

instance Num a => Num (D s a) where
  D x x' + D y y' = D (x + y) (x' + y')
  D x x' * D y y' = D (x * y) (x' * y + x * y')
  negate (D x x') = D (negate x) (negate x')
  abs    (D x x') = D (abs x) (signum x * x')
  signum (D x _)  = lift (signum x)
  fromInteger x   = lift (fromInteger x)

instance Fractional a => Fractional (D s a) where
  recip (D x x') = D (recip x) (-x'/x/x)
  fromRational x = lift (fromRational x)

Because the phantom type s is part of the type of a number, and because arithmetic operations such as + require the arguments and the return value to have the same type, it is a type error to add numbers denominated in different infinitesimals. In particular, the erroneous definition reflectBug above is now a type error, as desired.

Occurs check: cannot construct the infinite type: t = D s t
  Expected type: t
  Inferred type: D s t
In the first argument of `lift', namely `(curve (x + h))'
In the expression: lift (curve (x + h))

For this checking of infinitesimal units to be sound, this library for automatic differentiation should not export the values D and infinitesimal to its users, though of course the type constructor D and its type-class instances need to be exported, along with the functions d and lift.

(In the discussion that ensued, David Roundy noted that the same kind of static safety can be achieved by exporting just a function

d :: Num a => (forall b.
      Num b => (a -> b) -> b -> b) -> (a, a)

for differentiation. The type b makes it unnecessary and useless to export the type constructor D, even though d is still implemented using D. Also, the new argument of type a -> b makes it unnecessary and useless to export the lift function. Finally, the type-class context Num b makes it unnecessary and useless to export the Eq, Show, and Num instances for D. However, as Chris Smith lamented, we need additional differentiation functions of the types

Fractional a => (forall b.
 Fractional b => (a -> b) -> b -> b) -> (a, a)

Floating a => (forall b.
 Floating b => (a -> b) -> b -> b) -> (a, a)

in order to differentiate functions that use Fractional or Floating operations. Oleg Kiselyov used similar types to express symbolic differentiation.)

Automatic lifting

Although the type system now prevents us from putting calls to lift in the wrong place, it is still annoying to have to invoke lift manually—especially for nested differentiation, a useful case as discussed above. Depending on ‘how constant’ a quantity is, we need to feed it through a composition of exactly the right number of lifts. This manual coding is frustrating because the unique right number of lifts to apply is obvious from the input and output types desired: to convert a type a to the type D s a, apply lift once; to convert a to D s (D s' a), apply lift twice; and so on. We want the compiler to manage these subtyping coercions automatically.

An analogous situation arises with state threads, which can be organized into a hierarchy of memory regions. As part of a monadic computation that uses mutable cells in a parent region, we can create a child region and perform a subcomputation that allocates and accesses mutable cells in both regions. After the subcomputation completes, the child region is destroyed en bloc, but we can still use the parent region and observe any effect on it brought about by the subcomputation. To allow the subcomputation to use the parent region, we want every region to be a subtype of its descendents. Matthew Fluet and Greg Morrisett’s implementation of nested regions in Haskell uses explicit subtyping coercions just like our lift: depending on ‘how senior’ a region is, we need to compose exactly the right number of region coercions.

In a pending submission to the Haskell symposium, Oleg and I show how to automate region subtyping coercions using type classes. One might hope to apply that approach to lifting in automatic differentiation. Indeed we can, but I only know how to automate counting lifts, not how to automate placing them. That is, instead of feeding each use of an input quantity to the lift function exactly the right number of times, we can feed it to a new function once. The new function, called lifts, belongs to a new type class Lifts, which takes two type parameters. The constraint Lifts a b holds if and only if the type b is the result of applying zero or more type constructors D s to the type a.

class Lifts a b where
  lifts :: a -> b

More concretely, the following instances incompletely approximate the intended meaning of Lifts.

instance Lifts a a where
  lifts = id

instance Num a => Lifts a (D s a) where
  lifts = lift

instance Num a => Lifts a (D s (D s' a)) where
  lifts = lift . lift

instance Num a => Lifts a (D s (D s' (D s'' a))) where
  lifts = lift . lift . lift

The definition above of reflect in terms of d applies lift once to one occurrence of x but not to other occurrences of x and h. The same function can be expressed using Lifts, by applying lifts once to each occurrences of the input variables x and h.

reflectAuto :: Fractional a => a -> a
reflectAuto x
  = let (y,y') = d (\h -> curve (lifts x + lifts h))
    in y + lifts x * (recip y' - y') / 2

Expressing reflect in this new way frees us from counting how many times to lift the inputs x and h each time they are used.

How to implement Lifts? On one hand, as an implementation of Lifts, the approximate instances above are incomplete and unsatisfactory in theory, in that they restrict how many lift each lifts can stand for. They are perfectly useful in practice, however, and rely on no extension to Haskell other than rank-2 types and multiparameter type classes with flexible instances. On the other hand, a complete implementation is possible using the TypeCast class for type improvement (originally used by Kiselyov, Lämmel, and Schupke to implement heterogeneous collections), but it requires more Haskell extensions: functional dependencies, overlapping instances, and undecidable instances. Without further ado, below is the complete implementation.

instance Lifts a a where
  lifts a = a

instance (TypeCast (D s b') b, Num b', Lifts a b')
  => Lifts a b where
  lifts = typeCast . lift . lifts

class TypeCast a b | a -> b, b -> a where
  typeCast :: a -> b
class TypeCast' t a b | t a -> b, t b -> a where
  typeCast' :: t -> a -> b
class TypeCast'' t a b | t a -> b, t b -> a where
  typeCast'' :: t -> a -> b
instance TypeCast' () a b => TypeCast a b where
  typeCast x = typeCast' () x
instance TypeCast'' t a b => TypeCast' t a b where
  typeCast' = typeCast''
instance TypeCast'' () a a where
  typeCast'' _ x  = x

Although Lifts makes it easier to use automatic differentiation, this implementation is heavy lifting. I wonder if it is easier to express this combination of subtyping and rank-2 polymorphism in a language like Scala?