Very far away from anywhere else

My experience immigrating to a foreign place is inextricable from my experience growing up. Somewhere along the way I learned the habit of recoiling from disappointment by lowering my expectations to match. I shrunk myself in space and time, never delaying others by holding the subway door open. As I practiced attending to the present and the internal, I dissociated from planning for the future and trusting the external. What’s beyond my arm’s reach is not my home and I don’t belong there. If I don’t have time to make a vegetable available by growing it myself, then it doesn’t deserve to be my comfort food.

People say they don’t recognize their country anymore. I just realized that in my case, it’s myself that I don’t recognize anymore.

Double blind

Whether and why and how to double-blind depends on what we’re trying to do together, what’s just, and what’s humanly achievable—all assumptions hard to pin down even if folks are willing. But here’s how I think about it.

Suppose we want to estimate the effect of reading a given paper on a person. Maybe this is because we want to decide whether to publish a paper, to promote its authors, or whatever. In the first sentence of this paragraph, I sneaked in the generic noun phrase “a person” as if there is a given person, but in fact there is a distribution over persons (possibly current and future, real and fictional) that we care about. A typical approach to this estimation task is to feed the paper to persons who we hope can both represent the intended audience (by being a member, modeling the members, or both) and report their experience (by writing a review with evaluation, advice, or both).

The estimation cannot be perfect as long as the reviewing panel is not exactly same as the audience. In fact, a reviewer may well not be a typical audience member. For example, it is folklore that a research paper should be written for a first-year graduate student, but most reviewers are not first-year graduate students. This can make sense because a skilled and knowledgable reviewer may be able to model a typical audience member without being one. Still, no reviewer or reviewing process is omniscient (or perfectly rational (or perfectly altruistic)). Reviewers could use help—perhaps in the form of oxygen, coffee, or double-blinding.

On this view, I expect (which is not to say that others should expect) double-blinding to help if our intended audience contains lots of people who don’t know the authors and their research trajectories, so that a reviewer could better model how those people would react to the paper. As I said above, the precise audience is hard to pin down, but those people might include first-year graduate students as well as the fictional reader named “model-theoretic semantics” who evaluates a paper for “truth”.

(Thanks to Tim Chevalier for prompting me to write this.)

Derailing

A type checker that derails:
”show :: a -> String”
“OK”
”x :: Int”
“OK”
”show x”
“but you can’t show functions”

A proof checker that derails:
“Birds fly. Tweety the Canary is a bird. So Tweety flies.”
“But Fido the Ostrich doesn’t fly.”

---

Another type checker that derails:
”main = putStrLn s”
“OK, how about s = show id”

Another proof checker that derails:
“Fido doesn’t fly.”
“But Fido is a bird, and birds fly.”

---

A helpful type checker:
”show id”
“but you can’t show functions”

A helpful proof checker:
“Birds fly. Fido is a bird. So Fido flies.”
“But Fido is an ostrich, and ostriches don’t fly.”

---

Another helpful type checker:
”main = putStrLn s”
“OK, how about s = show 42”

Another helpful proof checker:
“Tweety doesn’t fly.”
“But Tweety is a bird, and birds fly.”

A challenge for a better community

Did you know that all ACM-sponsored conferences have an anti-harassment policy? I didn’t, until I chaired the Haskell Symposium last year. The concise policy says, among other things, that people shouldn’t use my family constitution to interfere with my professional participation. And the policy has teeth. That’s great.

My not knowing the policy and not seeing it publicized didn’t make me go out of my way to harass anyone. But it did make me less sure and less comfortable that I belonged at ICFP. Briefly, it’s because I didn’t know if it would be common ground at the conference that my actual self was fully human. That’s not something I can take for granted in general society. Also, it’s because I didn’t know whether my fellow conference attendees were aware of the policy. We could all use a reminder, and a public signal that we mean it.

For these reasons, I’m very happy that ICFP will start to publicize ACM’s existing anti-harassment policy and make sure everyone registered knows it. All ACM conferences should do it. That’s why Tim Chevalier, Clement Delafargue, Adam Foltzer, Eric Merritt, and I are doing two things. We ask you to join us:

1. Donate to the Ada Initiative. Our goal is for the functional programming community to raise $8192 by the end of Friday (Sept 19) UTC. To count toward this goal, please use this link: http://supportada.org/?campaign=lambda
2. Call on the ACM and tell your friends. For example, I tweeted this:
   I donate to @AdaInitiative because I want @TheOfficialACM events to announce their anti-harassment policy http://supportada.org/?campaign=lambda #lambda4ada

Thanks for improving our professional homes!

(UPDATE: Wow! We reached our initial goal $4096 in just 5 hours! We increased the goal to $8192, thanks to your generosity. And if we raise $16,384, we will sing ”There’s no type class like Show type class” and put a recording on the Internet.)

Haskell Symposium program chair report

Thank you all for coming! There are about 160 people registered for the symposium, which includes about 130 people registered per day.

Thanks to everyone who submitted a paper! We received 37 papers [UPDATE: I misspoke; the actual number is 33], of which we accepted 13. Unfortunately, we could not accept the 2 of those submissions that were functional pearls, or the 2 of those submissions that were experience reports. I’m not sure what’s going on or whether we should do anything about it.

We received 4 demo proposals, and accepted 3 of them. We received 0 panel proposals, and accepted 3 of them. I mean, all the panels were the results of direct soliciting. There were 2 panels yesterday and 1 today. I don’t know if panels were a good idea; more on that later.

Each paper received at least 3 reviews. Thanks to the 16 PC members and 16 external reviewers who produced those thoughtful and informative reviews on a very tight schedule. Please give them a hand.

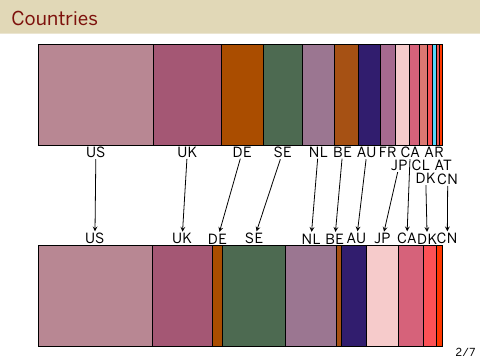
Here is a chart of the countries of authors of submitted papers (at the top) and of accepted papers (at the bottom). You can see the usual suspects to the left, and also to the right there were authors from Chile, Denmark, Argentina, Austria, and China, but only the papers from Denmark and China made it.

This year the symposium went to 2 days from 1 day, and the panels are new, and the keynote is new. I have no idea what you think of these format changes. I don’t even know many of you. So please take this survey (just take the URL of the symposium and put the word “survey” at the end) and let us know what you think!

Again, thanks to the program committee, especially to Norman Ramsey for his sage advice.

Thanks also to the steering committee, especially to Jeremy and Janis for their sage advice. Of course, this would not happen without the local organizers, starting with Greg Morrisett, and the workshop chairs, Patrik and Sam.

Thank you for coming, and thank you for caring so much about Haskell that you even came to a PC chair report at 9am. Thank you also for making the Haskell community such a welcoming place. Any questions?

I want to talk about the pain and pleasure of the Haskell community. The Haskell community is not such a welcoming place to a significant number of people. Regarding this, let me recall something Simon Peyton Jones said a long time ago. He was talking about how to write papers and handle reviews, but I think his advice applies just as well to personal interactions and the difficult task of communication in general.

I want to remind ourselves, starting with myself, to be grateful for criticism as well as praise. Because we are among friends—friends who inspire us to do our better, to do our best.

So I want to remember to interpret criticism as suggestions for improvement. Let’s thank those friends warmly, because they have given up their time. for us.

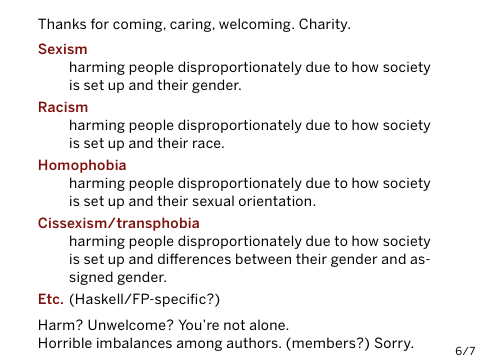
There are some specific ways in which the Haskell community has not been welcoming. We have harmed people disproportionately—I know; I have talked to them—due to how society is set up and their gender. We have harmed people disproportionately due to how society is set up and their race. Or their sexual orientation. Or differences between their gender and assigned gender. Or maybe due to the fact that not everyone grew up in their parents’ garage hacking category theory at age 14.

So, if you see harm—if you feel unwelcome—you. are. not. alone.

I showed you the country chart earlier. I didn’t show you the gender chart or the race chart, because I can only do so many sad things per day. There are horrible imbalances among the authors of this symposium. I think there were like two women. Of course you don’t have to write a paper to be a member of our community, but this is a tip of an iceberg. And I’m sorry for the tip and I’m sorry for the iceberg. I should have instituted double-blind reviewing and I didn’t. I’m sorry for that.

So what should we do about it? What am I doing about it? I want to tell you quickly about two things.

First, it’s high time we learned from those people who did not find the Haskell community a welcoming place. If you were excluded, or if you know someone who was, please share your stories. Of course you don’t have any obligation to do anything, but out of the goodness of your hearts, please be our teacher. Please contact me, at ccshan@indiana.edu. I’m getting help from some cultural anthropologists at Indiana University. If you know about anthropology at Indiana, you’ll know that these are professionals who really know how to learn from and respect your individual experiences and perspectives. We’re going to conduct interviews and anonymize them. Then, I’m not sure what we’ll do with the interviews—maybe they’ll become a SIGPLAN Notices article, or a theatrical play, or a shared resource if the interviewees are willing. In any case, the goal is to strengthen our empathy for each other, to understand our different perspectives on our shared community, and to open conversations about this important topic.

Second, as we have those conversations—indeed, whether we’re having a technical conversation or a social conversation, and whether it’s a communal discussion or a private one-on-one, let us: Be friendly, and speak our minds with compassion. Let us be charitable, and listen to others with compassion. Let us support one another, whether by speaking up or stepping back. And let us not burn out, and take care of ourselves, because this is hard, worthwhile, work. Just like it’s worthwhile to hack GHC or to write a clear paper or to give a sincere talk or to ask a helpful question or to write a respectful message on haskell-cafe or to glue together PHP and shell scripts to hold up our community infrastructure. None of us signed up for this work when we were born—I didn’t sign up for my native language to be the one not made fun of at my elementary school—so thank you for doing it.

Thanks to three amazing women—Ava DuVernay, Lindsey Kuper, and MrsB—for inspiring me to talk about this, and thanks to the SIGPLAN executive committee for their support.

I have time for a couple of short questions.

Borderline, just semantics

I want to discuss two moral aspects of how to talk about borderline people (e.g., whether to say “MTF” or “female”, “smart” or “good at math”).

The first aspect is what category of people we should be talking about, never mind how we talk about it. Usually, for a given category C, there are many ways to be borderline C: people can be

• borderline female due to a lack of chromosomes or a lack of genitals;
• borderline smart because they keep exchanging quantifiers or because they keep estranging family;
• borderline safe because they drive over the speed limit or roll their bike past a stop sign;
• borderline documented because they burned their passport, overstayed their visa, or came from an unrecognized “country”.

Of course, it is easy enough to construct a category C’ that firmly includes or excludes particular kinds of borderline Cs (e.g., you are female’ iff you have XX chromosomes), if only to leave unresolved lower-dimensional borderlines (e.g., what if only half of your cells have XX chromosomes). So let’s ask not what categories exist (because they all do) but what categories we should talk about.

It might well be that we should talk about different versions of C for different purposes (e.g., medicine, sports, identification, love). It might also be that delineating categories at their edges is not usually worth our collective cognitive trouble. Regardless, sometimes in conversation or other collaboration I find that multiple versions are actually relevant. For example, some people wonder whether to call a transgender person “male” or “female”, and I think a transgender person can firmly belong to a gender category that we should talk about. Unfortunately, when I tried to work with others to distinguish and choose among versions of categories, I have often been frustrated.

When people in power to classify others don’t take the effort to apply the right category version, the misclassified people can get slighted. I empathize with the misclassified people because I have been misclassified—for example, I don’t need a passport to travel internationally, and I am a computer scientist.

The second aspect is how to name a given category (version). Even in a context where we agree intellectually that there is exactly one gender category we should talk about (say “female”) and a transgender person belongs to it firmly, the term “female” still takes many people today more thought to produce and comprehend when applied to a person known to be transgender than when applied to a person known to be cisgender. So, it is tempting for a well-meaning speaker to avoid gender categories altogether by terming a transgender person “female-presenting” instead. The “female-presenting” characterization

• is certainly true,
• but may be a cop-out because it
  • perpetuates the implicature that the person doesn’t quite belong
  • and increases their work to counter misclassification,
• yet may be justifiable (perhaps in some strain of utilitarianism), though a justification remains to be spelled out and applied uniformly to all instances.

Your thoughts?

Why not covariant generics?

Many people are riled up that Dart’s type system proudly features covariant generics and so “is unsound”. The basic problem with covariant generics is that it lets you take a bowl of apples and call it a bowl of fruit. That’s fine if you’re just going to eat from the bowl and you like all fruits, but what if you decide to contribute a banana to the fruit bowl? Someone taking from the bowl expecting an apple might choke. And someone else could call the same bowl a bowl of things then put a pencil in it, just to spite you.

… because they are unsound?

We all seem to agree that it’s bad for an apple eater to choke on a banana or a fruit eater to choke on a pencil. (Wittgenstein and Turing similarly agreed that it’s bad for a bridge to fall and kill people.) For example, Java seems to agree: it detects at run time when such choking is about to occur and throws an exception instead, so no immediate harm is done. There is less agreement as to whether a static type system must prevent such choking before run time. One argument for early prevention is that it’s the whole point of having a static type system—why even bother with a static type system if it’s unsound?

But plenty of static type systems are unsound yet respectable. For example, many dependent type systems are unsound, either because their term languages are blatantly non-terminating or because they include the Type:Type rule. (I faintly recall that Conor McBride calls Type:Type “radical impredicativity”.) So it doesn’t seem that unsoundness per se should rile people up about Dart in particular.

Perhaps it’s time to distinguish different sorts of unsoundness: a type system can be unsound because it fails normalization or because it fails subject reduction. In the former case, a program (or the type checker) might promise an apple but never produce one; in the latter case, the program might promise an apple then produce a banana. The unsoundness of a dependent type system tends to be of the former sort, whereas the unsoundness of covariant generics seems to be of the latter sort. And the former sort of unsoundness seems more benign than the latter sort (and more deserving of the term “radical impredicativity”). So, by calling for subject reduction but not normalization, it seems we can drive a wedge between the acceptable unsoundness of many dependent type systems and the unacceptable unsoundness of Dart.

But it is very easy to turn a failure of subject reduction detected at run time into a failure of normalization: just go into an infinite loop whenever choking is about to occur! In Java, we can write catch (Exception e) { for (;;) {} }. (In math, we can restore subject reduction by letting an uncaught exception take any type, as is standard.) Is that really better? Does this move really answer the critics? I don’t feel so. For one thing, this move makes it harder, not easier, to write better programs: I want my program to stop and tell me when it’s choking.

Just as it’s only useful for type systems to allow a program if it’s something good that a programmer might write, it’s only useful for type systems to disallow a program if it’s something bad that a programmer might write. In other words, both incompleteness and unsoundness “may appear to be a steep price to pay” yet “work well in practice”. Does Type:Type abet many bad programs that people produce? Perhaps not. Do covariant generics abet many bad programs that people produce? Perhaps not. Are untyped bowls and naive set theory terribly dangerous? Perhaps not. (Proof rules and programming facilities that are unsound may even encourage useful abstraction and reduce the proliferation of bugs by copy-and-paste.)

… because they are meaningless?

To summarize so far, I don’t think we should dislike covariant generics for its unsoundness in general or for its failure of subject reduction in particular. Why do covariant generics bother me, then? I think it’s because they dash my hope for types to have crisp meanings.

When I write down an expression, whether it’s a term or a type, I want it to refer to something else, whether in my mind or in the world. When I write that a certain term has a certain type (say, alice:person or 2+3:nat), I want to write about some entity, to mean that it has some property. That is not subject reduction, but to have a subject and a predicate in the first place, which is prior to subject reduction. I would be dissatisfied if there is no subject and predicate to be found outside the syntax and operational semantics of a formal language. After all, my desire to assert that 2+3:nat is not fueled by any interest in the curly symbols 2 and 3 or the binary node label +. In short, I want to denote.

Of course, it’s not entirely a formal language’s fault if I can’t use it to denote, if it’s hard to program in. Syntax only goes so far, and cognition must carry the rest of the way. But it does get easier to denote and program if how expressions combine inside the language matches how their referents tend to interact outside the language. For example, FORTRAN made it easier to denote numbers than in assembly language: having written 2+3 to denote a number, and knowing that numbers have absolute values, I can write abs(2+3) to denote the absolute value of the number denoted by 2+3. Numbers are outside FORTRAN, yet FORTRAN matches my knowledge that numbers have absolute values. In contrast, if you can hardly put a banana in a bowl of apples in reality but you can easily put(banana, bowl:Bowl<Apple>) in formality, or vice versa, then I have trouble seeing what banana and bowl mean.

This match I want is a kind of modular reasoning. Now, the word “modular” has been used to mean many things, but what I mean here is this. To combine two objects inside a language, I might need to worry about whether their types match, whether they live on the same machine, whether they use the same calling convention, etc. To combine two objects outside a language, I might need to worry about how big they are, whose kitchen it is, and whether fruit flies would come. Ideally, my worries inside the language should match my worries outside the language. Ideally, a combination should make sense inside a language just in case the referents of the combined expressions are compatible outside the language. If the language implementation could keep track of my worries and discharge them as early as possible for me, then so much the better, but that’s secondary and orthogonal—I’d be plenty happy if I can just talk about worrisome things without also worrying about the language at the same time.

I feel it’s hopeless to match a language with covariant generics against things we want to talk about. Why? I don’t have proof. For all I can show, the worries of a Dart programmer inside and outside the language will match perfectly, just as Java exceptions precisely simulate the material effects of putting a pencil in a bowl of apples. In the end, my feeling boils down to the unreasonable and unusual effectiveness of mathematics and logic.

Not only might this effectiveness be fallible, but it’s also possible that my hopelessness is misplaced. I said I want expressions to match their referents more closely so that denoting and programming becomes easier. But maybe the match we have today is the best we can do because the world has too many shades of gray to be modeled in the black-and-white terms provided by mathematics and logic. Maybe the world simply refuses to provide crisp referents for any expression to mean. Maybe, when lexical references slip and uncaught exceptions fire, it’s just collateral damage from the fact that life is messy. After all, it is one thing for a bridge engineer to leave gravity unquantified because calculus is hard; it is another thing for a bridge architect to leave beauty unquantified because psychology is hard. To avoid variance rules just because they ”fly in the face of programmer intuition” feels like the former to me, but what do I know?

… because they are not even unsound?

Well, I do my best. I do my best to understand whether and how reference and truth can help programming. I do my best to enlist syntax and pragmatics. I’m not yet ready to give up just because so many people are confused by noun-noun compounds in English (what’s an “apple bowl”?) and by variance rules in Java today. To me, the notion of being sound or unsound only makes sense if expressions have meanings outside the language. I do my best so that Bowl<Apple> means something, so that when I claim ”it is easy for tools to provide a sound type analysis if they choose” I know what I mean by “sound”. To not even worry about what expressions mean is not even unsound.

(Rob Simmons beat me to a blog post. He makes good, related points.)

Goodbye Rutgers

”FREE BOOKS! by taking them away” I wrote on my office door. I had an hour before my next appointment to reduce my life at Rutgers to a carry-on suitcase. So I had to leave behind everything that I can buy again, even those volumes soaked with memories: my first linguistics class, my first book chapter, conferences where colleagues blew me away with their wit and intellect. You know, you’re all mentors to me.

Sorting the shelves gave me the thrill of picking an old ripe scab. Like a sudden disaster that engulfs your house, like a subway door that closes after you and shuts out a latecomer, the scythe made me declare which arm belongs to my memories and which leg belongs to me. Highly recommended.

After all, books (like children and love) are better free.

This fall semester, I’m excited to be visiting Cornell linguistics, home of Mats Rooth’s computational linguistics lab. For excitement in the spring, I plan to visit Tsukuba computer science, home of Yukiyoshi Kameyama’s programming logic group. For both of these opportunities, I am grateful. After them, all bets are off. I want to keep learning and teaching, whatever that means. Maybe it’s time for me to work on a new citizenship. I’m open to suggestions.

The sun is brilliant. I didn’t just run into an old friend yesterday. I was also delighted to experience Bollywood for the first time, to get a tooth crowned for the first time. I won’t just meet up with an older and younger friend tomorrow. I will also be delighted to hear a new talk, to find a new thought.

TPDC 2011

I was honored to be an invited speaker at the Workshop on Theory and Practice of Delimited Continuations last month. The organizers—Alexis Saurin, Hugo Herbelin, and Noam Zeilberger—did a great job at putting together a friendly and informative event. Here are some fragmentary notes.

Zena Ariola, Hugo Herbelin, David Herman, and Dan Keith: Let’s change the abort in Filinski’s implementation of shift/reset from strict to lazy. (1) When a top-level reset is present as there is supposed to be, the implementation still works as specified. (2) Moreover, in the unspecified situation where there is no top-level reset, the implementation behaves more consistently.

Pierre Boutillier and Hugo Herbelin: Types better not depend on impure terms, so require reset around terms that occur in types.

Noam Zeilberger: Presheaves are {a fancy name for, the constructive content of, the result of categorifying} Kripke semantics. Kripke’s worlds and their relationships are the objects and morphisms of the category that the presheaf is a functor from. Can we identify the dependency in dependent types with the dependency in evaluation order?

Roshan James and I debated the computational content of the movie Primer. The question boiled down to this: using the mechanism in the movie, can you build (a la “Constraining Control”) a box that reports how many times it has been used, total (throughout all time)? My answer is no because I model the movie using the following monad, which I should explain in writing some day:

data Tree a = Leaf a | Branch (Tree a) (Tree a)

newtype Primer w a = Primer ((a -> Tree w) -> Tree w)
instance Monad (Primer w) where
  return a       = Primer (\c -> c a)
  Primer m >>= k = Primer (\c -> m (\a ->
                   let Primer n = k a in n c))
runPrimer :: Primer w w -> Tree w
runPrimer (Primer m) = m Leaf

data Box w a = Box { exit :: Maybe a
                     , enter :: a -> Primer w () }
newBox :: Primer w (Box w a)
newBox = Primer (\c ->
  let enter a = Primer (\c' ->
                Branch (c' ()) (c (Box (Just a) enter)))
  in c (Box Nothing enter))

Moe Masuko and Kenichi Asai implemented shift/reset in Caml Light. Their group is writing many interesting programs on top of this platform (such as declarative game-strategy search with alpha-beta pruning). Masuko’s and Herbelin’s presentations made me think it might make more sense to put one big reset around the entire REPL rather than one reset around each REPL interaction. This way, in the typical REPL that allows creating new top-level bindings using “let”, if we accidentally shadow a binding with another of the same name, we could still get back the old binding by invoking a previously captured REPL continuation.

Roshan P. James and Amr Sabry: yield is popular, and people even speak of it as a “delimited I/O” facility. I wonder if the popularity is because the type of yield is first-order?

General discussion

Christophe Calvès’s PhD thesis has a part about a hierarchy of monad transformers. Filinski’s recent paper “Monads in Action” presents an operational model of side effects in which monads are dynamically layered. Implementing this model in terms of shift/reset (with a proof of correctness and all that) would be nice and is an open problem as far as we know! In particular, we’d like dynamically layered regions of monadic effects.

Speaking of layering: The examples we currently have of using cupto/set in practice all have the flavor of making one present-stage (aka metalanguage) prompt/cell per future-stage (aka object-language) binder:

• Balat et al.’s “Extensional Normalisation and Type-Directed Partial Evaluation for Typed Lambda Calculus with Sums”
• Label every binder in a λ-term with how many times that bound variable is used
• Transform a λ-term to make contraction explicit, for example turning “λx.xx” into “λx. let x₁=x and x₂=x in x₁x₂”

So, if we represent the input term by “de Bruijn Notation as a Nested Datatype” (Bird and Paterson), can we write any of these examples using a control hierarchy like Danvy and Filinski’s that makes the absence of uncaught shifts patent to the type system? The use of type-level functions and polymorphic recursion is allowed.

What is the distinction between undelimited and delimited continuations? Führmann’s thesis concerns the distinction? I feel the important distinction is whether an expression is polymorphic or not in the answer type.

What is a continuation, some reviewers ask? I take the “continuation stance” (cf Dennett’s intentional stance) when appropriate: something is a continuation when a direct-style transformation that makes it implicit simplifies the program overall. In the end the answer depends on what is representation.

Conversations outside the workshop

Olivier Hermant explained deduction modulo to me: augment first-order logic with equations or rewriting rules to capture things hard to express in first-order logic such as transitivity or arithmetic. Uniform metatheoretic results such as proof normalization across many modulo. Is this tool good for natural logic?

Peter Dybjer is hooking up Agda to first-order automatic theorem provers. The idea is to describe the existence of an Agda proof as a first-order formula, so if the theorem prover says yes then you trust that there is an Agda proof. This way, hopefully the end user of Agda only needs to give the broad outlines of a proof like what induction or pattern matching to do.

TLCA papers to read: “Classical Call-by-Need and Duality” (Ariola, Herbelin, and Saurin), “Game Semantics and Uniqueness of Type Inhabitants in the Simply-Typed Lambda-Calculus” (Pierre Bourreau and Sylvain Salvati), “A Filter Model for λμ” (Steffen Van Bakel, Franco Barbanera, and Ugo De Liguoro).

I agreed with Barry Jay that “well typed” and “simply typed” should never be hyphenated, but then I wondered: do these phrases perhaps have specialized meanings that justify hyphens?

Train go sorry

There are two kinds of people, those whose utterances have truth conditions and those whose utterances are jokes. (Thanks to David Beaver.)

I was on the NJ Transit train from New York to SALT at Rutgers. A lady and a guy got on at the airport.

• Conductor to guy, punching his ticket:
  This train doesn’t go to Foo. Get off at the next stop and change to a North Jersey Coast train.
• Guy to conductor:
  Oh! They told me to go to Track 5. So this train doesn’t go to Foo?
• Conductor to guy:
  No, change at Rahway, the next stop.
• Guy to conductor:
  Ok. Thanks.
• Guy to lady:
  Excuse me, do you know how I can find out which train goes to Foo?
• Lady to guy:
  Sorry, I don’t know. I’m a visitor myself.
• Me to guy:
  Where are you going? Which train are you trying to take?
• Guy to me:
  I thought this train went to Foo. They told me to go to Track 5.
• Me to guy:
  Oh, you have a North Jersey Coast line schedule in your hand. Let’s see. Which train are you trying to take?
• Guy to me:
  I want to go to Foo. (points index finger all over schedule) How I can find out which train goes to Foo?
• Me to guy:
  You need to read the schedule. Let’s see… (realizes he needs to get off at the next stop) Sorry, there’s no time for me to tell you how to read the schedule. But in short, you need to read the schedule. That’s how you find out which train goes to Foo. By reading the schedule.
• Guy to me:
  Ok, thanks. The guy at the airport just told me to go to Track 5. I thought this train goes to Foo.
• Me to guy:
  Every train to Foo is on Track 5. That doesn’t mean that every train on Track 5 goes to Foo.
• Guy to me:
  Oh, but the guy told me to go to Track 5. Thanks.
• Guy gets ready to exit the train and ponders schedule for a few seconds.
• Guy to me:
  So I should look for trains marked with Q?
• Me to guy:
  Q? What Q?
• Guy to me:
  Here on the schedule it says: “Trains marked with Q”
• Me to guy:
  Let me look. Oh. (enters office-hour mode subconsciously) Please read that sentence.
• Guy to me:
  “Trains marked with Q”
• Me to guy:
  Ok, keep reading, the sentence hasn’t ended yet.
• Guy to me:
  “Trains marked with Q are part of NJ Transit”
• Me to guy:
  But the sentence hasn’t ended yet. Keep reading. Please finish.
• Guy to me:
  “Trains marked with Q are part of NJ Transit’s Quiet Commute program.”
• Me to guy:
  Right. That’s the whole sentence.
• Guy to me:
  I thought my train is part of the Quiet Commute program.
• Me to guy:
  (flabbergasted) … Why do you think that?
• Lady to me:
  Excuse me, why don’t you just help the poor guy. He’s just trying to get somewhere. You’re trying to get him to read but it would be so much more helpful if you tell him which train to take, how to get to his destination. You’re not being helpful.
• Guy to lady and me:
  I don’t know what’s going on. I just came from Canada.
• Lady to me:
  Yeah, instead of being unhelpful, why don’t you answer his question.
• Me to lady:
  What was his initial question to me?
• Lady to me:
  He asked how to get to Foo.
• Me to lady:
  That was not his question.
• Guy to lady and me:
  Sorry to bother you; thank you very much; bye.
• Lady and me to guy:
  Bye.
• Guy exits.
• Me to lady:
  I’d love to talk about this over tea.
• Lady to me:
  I just don’t think it’s helpful to teach him to read the schedule when he’s just trying to get some place. Why don’t you tell him what to do.
• Me to lady:
  I’d love to talk about this, but it may take a while. I’m getting off at New Brunswick. Do you want to talk for a few minutes?
• Lady to me:
  (grin dismissal) No.
• Me to lady:
  Don’t start conversations that you don’t intend to continue.
• Lady:
  Tch.

We actually did stop talking from then on.

(ps. I wasn’t trying to hit on the lady.)

Art meets science

Art Meets Science is an exhibition of quilts inspired by science. It is worth an hour of your time to see. Until 2011-03-16, it is on view at 235 E 42 St, New York City. The building is Pfizer’s; to see the exhibit, you need to email Ms Therese Sathue two days in advance with your name and the date and approximate time of your planned visit.

Most of the 35 beautiful quilts on display are inspired by the physical sciences. Many of the images are biological and relate beauty and death. Several placards describe the copyright status of sources but leave out much of the rest of the quilts’ provenance. Not all of the inspiration is physical, though—there are references to Sierpinski and Fibonacci. By the way, does the definition of a fractal really require self-similarity? Surely having fractional Hausdorff dimension does not require self-similarity.

Hat tip to Nina Paley, who is jumping into quilting with a splash. She increased my appreciation for these quilts by letting me try using a sewing machine for the first time!

The extensible visitor pattern in tagless final style

This literate Haskell program translates Shriram Krishnamurthi, Matthias Felleisen, and Daniel P. Friedman’s “extensible visitor pattern”. Their paper ”Synthesizing object-oriented and functional design to promote re-use” (ECOOP 1998, 91–113) proposes this pattern as a solution to the expression problem. Unlike them, we don’t use any type casts!

{-# LANGUAGE Rank2Types #-}

module ExtensibleVisitor where

data Point = Point { x, y :: Double }
  deriving (Eq, Show)

class ShapeProcessor a where
  square :: Double {-s-} -> a
  circle :: Double {-r-} -> a
  translated :: Point {-d-} -> a {-s-} -> a

newtype Render = Render (Int {-prec-} -> String -> String)
instance Show Render where showsPrec p (Render s) = s p
instance ShapeProcessor Render where
  square s =
    Render (\prec -> showParen (prec > 10)
      (showString "square " . showsPrec 11 s))
  circle r =
    Render (\prec -> showParen (prec > 10)
      (showString "circle " . showsPrec 11 r))
  translated d (Render s) =
    Render (\prec -> showParen (prec > 10)
      (showString "translated " . showsPrec 11 d . showChar ' ' . s 11))

> translated (Point 1 2) (circle 3) :: Render
translated (Point {x = 1.0, y = 2.0}) (circle 3.0)

newtype ContainsPt = ContainsPt { containsPt :: Point {-p-} -> Bool }
instance ShapeProcessor ContainsPt where
  square s                   = ContainsPt (\(Point x y) ->
                               0 <= x && x <= s && 0 <= y && y <= s)
  circle r                   = ContainsPt (\(Point x y) ->
                               x * x + y * y <= r * r)
  translated (Point dx dy) s = ContainsPt (\(Point x y) ->
                               containsPt s (Point (x - dx) (y - dy)))

> containsPt (translated (Point 1 2) (circle 3)) (Point 2 3)
True

newtype Shrink a = Shrink { shrink :: Double {-pct-} -> a }
instance (ShapeProcessor a) => ShapeProcessor (Shrink a) where
  square s       = Shrink (\pct -> square (s / pct))
  circle r       = Shrink (\pct -> circle (r / pct))
  translated d s = Shrink (\pct -> translated d (shrink s pct))

> shrink (translated (Point 1 2) (circle 3)) 10 :: Render
translated (Point {x = 1.0, y = 2.0}) (circle 0.3)

class ShapeProcessor a => UnionShapeProcessor a where
  union :: a {-s1-} -> a {-s2-} -> a

instance UnionShapeProcessor Render where
  union (Render s1) (Render s2) =
    Render (\prec -> showParen (prec > 10)
      (showString "union " . s1 11 . showChar ' ' . s2 11))

> translated (Point 1 2) (union (square 4) (circle 3)) :: Render
translated (Point {x = 1.0, y = 2.0}) (union (square 4.0) (circle 3.0))

instance UnionShapeProcessor ContainsPt where
  union s1 s2 = ContainsPt (\p -> containsPt s1 p || containsPt s2 p)

> containsPt (translated (Point 1 2) (union (square 4) (circle 3))) (Point 2 3)
True

instance (UnionShapeProcessor a) => UnionShapeProcessor (Shrink a) where
  union s1 s2 = Shrink (\pct -> union (shrink s1 pct) (shrink s2 pct))

> shrink (translated (Point 1 2) (union (square 4) (circle 3))) 10 :: Render
translated (Point {x = 1.0, y = 2.0}) (union (square 0.4) (circle 0.3))

> containsPt (shrink (translated (Point 1 2) (union (square 4) (circle 3))) 10) (Point 2 3)
False

---

Below is the part that uses rank-2 types. We only need them if we want to process the output of a processor multiple times.

newtype Shape = Shape
  { processShape :: forall a. ShapeProcessor a => a }
instance ShapeProcessor Shape where
  square s       = Shape (square s)
  circle r       = Shape (circle r)
  translated d s = Shape (translated d (processShape s))

newtype UnionShape = UnionShape
  { processUnionShape :: forall a. UnionShapeProcessor a => a }
instance ShapeProcessor UnionShape where
  square s       = UnionShape (square s)
  circle r       = UnionShape (circle r)
  translated d s = UnionShape (translated d (processUnionShape s))
instance UnionShapeProcessor UnionShape where
  union s1 s2    = UnionShape (union (processUnionShape s1)
                                     (processUnionShape s2))

test :: UnionShape
test = shrink (translated (Point 1 2) (union (square 4) (circle 3))) 10

> processUnionShape test :: Render
translated (Point {x = 1.0, y = 2.0}) (union (square 0.4) (circle 0.3))

> containsPt (processUnionShape test) (Point 2 3)
False

(It would be nice to overload the names processShape and processUnionShape. We can do that by reifying the type classes ShapeProcessor and UnionShapeProcessor as two types that belong to the same multiparameter type class.)

Pollution and taboo are a cultural discipline for enforcing realms of abstraction

To: Lukhnos D. Liu

I have been thinking about your blog post about making change rather than calling attention to it. It seems that many (perhaps most or all) important changes are successful exactly when people don’t realize that they exist. User interfaces are like that: if your users notice that there is an interface, probably the interface is not good. Infrastructure services are like that: the goal of the sewage system is to provide city dwellers the abstraction (or, illusion) of free disposal of waste. If people think about the sewage, then it has failed. It makes it difficult for governments to raise the money to maintain the infrastructure.

Programming languages are similar: if programmers notice that the facilities provided by the language are not “really what happens on the machine” then the language has failed. [Nowadays, when people assert that mutable state is really what happens on the machine, I ask them if they mean string theory or quantum field theory—ed.] For example, machine language is successful in that programmers rarely think about microcode; garbage collection is less successful in that programmers often think about pointer reachability. So, I advise my colleagues studying programming languages that they are doomed for obscurity, like individual petals of cherry blossom.

It seems, then, that the computer scientist’s notion of abstraction may be related to the anthropologist’s notion of taboo. Do you know about the book “Purity and Danger”? I plan to take a look at it.

[Perhaps infrastructure services and programming languages are either dirty or sacred so people avoid touching it: if you touch it, then either it defiles you or you defile it—ed.]

---

From: Lukhnos D. Liu

Yes, it’s about time for me to pick up the book again some time, too. Remember we talked about this “should we wear shoes if we are moving a piano across a Japanese living room [to a bathroom? ;)]” question? I mentioned this to a friend of mine who’s teaching anthropology at Tunghwa University, Hualien, and that’s the first title he came up with. We should make this into a puzzle game…

---

To: Lukhnos D. Liu

I thought about making it into a puzzle game, but my tentative ideas were all too depressing to be fun enough for an actual popular game. When I described the idea to one person, she said, “oh, you’re describing life.” Yes, perhaps life doesn’t make for a popular game.

Actual New York City traffic rules

You are responsible for not hitting whatever is in front of you, unless it is crossing against the light, unless it is stopped.

If you just passed a bicyclist, pedestrian, or slow moving vehicle, your personal green light lengthens by 3 seconds (5 seconds if you honked). If you are following a bicyclist, pedestrian, or slow moving vehicle, your personal green light lengthens indefinitely.

Nothing that is stopped can have right of way.

During a walk light, if a vehicle occupies the crosswalk wholly or partially, then the crosswalk dynamically extends to encompass all points whose shortest distance to the vehicle is less than the original width of the crosswalk. In extreme situations such as rush-”hour” Lincoln Tunnel traffic, this rule can cause originally disconnected crosswalks to touch, making it possible to cross a street or avenue diagonally.

You may travel against the light while someone adjacent does. (This rule is coinductive.)

One-way signs dictate the logical direction of vehicular travel, which is mapped to the physical direction of vehicular travel by an ensemble of nondeterministic transformations. In particular, reverse gear allows backing up to the previous intersection.

If a traffic light malfunctions so as to provide no unique indication, use the following combination chart to disambiguate.

Walk on the right. Especially around building corners.

Walk on the left; stand on the right.

Keep walking.

Whether as victim or perpetrator, a mobile object that is not a motor vehicle and that is not presently touching any motor vehicle is invisible to law enforcement. Even though we like to pretend otherwise.

OCaml types

On 2010-12-18T06:36:54-0500, Jesse Howarth wrote:

Say I have functions like so:

let rec foo (f: 'a ->'a) (x: 'a) : 'a =
  f x
and a (x: float) = x
and b (x: string) = x
and bar = foo a 1.0
and baz = foo b "a"

I get an error on the last line that foo is expecting a function of type float -> float because I called foo with a before calling it with b. If I swap the last two lines, I get an error saying that it expects a function of type string -> string because foo was called with b before calling it with a. It seems like once I call foo, it saves the type of the polymorphic variable 'a. This is bizarre to me.

Do you have any idea what the problem might be?

You can get around this problem by splitting up the one big ”let … and … and …” into ”let … in let … in let …”.

Why? My understanding is that OCaml separately type-checks each let and generalizes the resulting types. So if you write

let rec (f: 'a -> 'a) (x: 'a) : 'a = f x in ...

then OCaml would look at this single definition and say, let me figure out what type 'a can be. Well, 'a can be any single type, so I’m going to put f into the type environment with the polymorphic type

forall 'a.  ('a -> 'a) -> 'a -> 'a

Then, each time you use foo, in bar and baz, the type variable 'a can be instantiated differently. So, each occurrence of let triggers generalizing type variables into polymorphic types. That’s the key of the Hindley-Milner type system behind the ML family of languages.

When you write everything with and, OCaml looks at the whole set of definitions and tries to figure out what type 'a can be. Well, this time 'a cannot be any single type, hence the type error.

Remember this program from CS314 last year?

let twice = proc (f) proc (x) (f (f x)) in
(((twice twice) proc (y) -(y,1)) 0)

Because we didn’t have Hindley-Milner polymorphism, type-checking this program gives the same type error.

On 2010-12-18T17:05:37-0500, Jesse Howarth wrote:

Thank you for the response.

I changed the definition to:

let fn =
let foo (f: 'a ->'a) (x: 'a) : 'a = (f x) in
let a (x: float) = x in
let b (x: string) = x in
let bar = foo a 1.0 in
let baz = foo b "a" in 0

(It wouldn’t allow me to just do the let … in without wrapping it with let fn = … in 0, I think because I am defining at the base of a file.)

I’m still receiving the error. What’s interesting is if I change it to:

let foo (f: 'a ->'a) (x: 'a) : 'a = (f x)
let a (x: float) = x
let b (x: string) = x
let bar = foo a 1.0
let baz = foo b "a"

Then it will not complain.

This also works:

let foo (f: 'a ->'a) (x: 'a) : 'a = (f x)
let fn =
let a (x: float) = x in
let b (x: string) = x in
let bar = foo a 1.0 in
let baz = foo b "a" in 0

Your explanation makes sense, but what happens in and cases as far as type checking may also happen with in cases.

Hrm! Thanks for pointing this out. I think it has to do with your putting the type annotations on f and x and (foo f x)—if you just say foo f x = f x then it works with the ”let … in” sequence (but still not with ”let … and”).

In OCaml, 'a means “a certain type I hereby omit” rather than (as in Haskell) “a generic type variable”. For example:

    Objective Caml version 3.11.2

# let f (x:'a) : 'a = x + 2;;
val f : int -> int = <fun>

So it’s hard to annotate a function with a polymorphic type. I believe OCaml 3.12 tried to address this:

”Type variables can be bound as type parameters to functions; such types are treated like abstract types within the function body, and like type variables (possibly generalized) outside.”

Really understanding effects

To: Mike Solomon
Cc: Chris Barker, Jim Pryor

Thanks for starting this great discussion, whether the start was this month, this year, or this millennium.

Let me first invoke the usual hypothesis of cognitive science: the mind is a computer/program/algorithm so let the study of the mind be informed by the study of computers/programs/algorithms. A lot of Mike’s comments have direct analogues in programming languages and software engineering—lots of people question why monads and continuations are useful and point out that mutation and GOTO are intuitively easy to understand. So, it’s not clear to me that time spent writing typical programs on a computer is more beneficial or convincing than the same time spent writing, say, Montagovian fragments with paper and pencil.

The concern that is more convincing, and that functional programming, monads, and continuations help address, is how to write and maintain large and reliable programs. The claim that a given program or part of a program works, like the claim that a given Montagovian fragment or lexical entry works, is basically a theorem. It takes effort to formulate and justify such theorems, especially if we want to do it not only by example but also by rigorous reasoning. As we change and grow our program over time, we want to avoid repeating what is essentially the same effort for parts that have not changed or lexical entries that are analogous. For example, we might want to prove one lemma about all values of a certain type, or all transitive verbs. In sum, we want modular programming, modular testing, and modular reasoning.

By “module”, I just mean that you could swap one out and stick another one in without affecting what we care about in the rest of the system. Whenever two pieces of code or testing or reasoning are similar, we want to put the similar parts in a module so that we can reuse our work as we repeat and change the pattern. Monads are one kind of module that emerged when people got tired of writing similar programs and proofs over and over again. It’s just like in the rest of math: groups, vector spaces, etc.

On 2010-12-14T12:49:18-0500, Mike Solomon wrote:

I would agree that monads give a potentially unifying perspective. I was challenging the claim that without monads you can’t “really” understand mutation/dynamic update. Or, that functional programming gives the best way to understand mutation. This just seems wrong to me. Monads are notoriously difficult to understand, mutation is intuitively easy to understand.

That is, I would say: we already understood mutation, now we look at it from a different perspective to try better understand how to combine it with other effects.

Of course what I just wrote may not be what it means to ‘“really” understand mutation/dynamic update’. Nevertheless, I would suggest that to “really” understand something entails proving theorems about it that go beyond particular usage examples—at least, not just “this program gives the correct output on this sample input” but “this program part works on all inputs regardless of the rest of the program”.

As soon as we humans who get bored easily try to prove such theorems, we want to capture repeated patterns in our reasoning so as to avoid repeating them. (Hoare logic for reasoning about imperative programs is a great and successful example of such capture, even though it treats mutation specifically and not as a special case of a side effect.) Maybe understanding mutation even entails being confident in a program part that uses mutation and no other side effect, regardless of what side effects occur in the rest of the program.

One question I asked yesterday (last night) is whether the analogy between quantification and shift/reset yielded insight independent of what kind of semantics one gave for shift/reset: shift/reset can be understood operationally, as a reduction calculus. Can quantification? But maybe this is just what QR is. In general, is the transformation to LF a kind of operational semantics?

I would answer yes, yes, yes.

I take at least 3 lessons from programming-language semantics into natural-language semantics: First, there are different kinds of semantics, not only denotational but also operational and axiomatic, each good for different purposes. Operational makes it more obvious how much time and space a program will take; denotational makes it easier to substitute equals for equals in a larger program. Second, we should relate the different kinds of semantics. For example, I’m a big fan of Olivier Danvy’s work on mechanically turning denotational semantics (well, definitional interpreters) into operational semantics or back. Imagine putting towers into a vending machine and getting QR out or vice versa! Finally, it is worth applying specific ideas such as monads in denotational semantics and evaluation contexts in operational semantics.

Is it only from the point of view of continuations that one can understand (best) a programming language that contains control and state?

Continuations are the best denotational account of control. It makes it easy to prove that the following expressions can be substituted for each other:

(shift c (and (c (mother 'john)) (c (mother 'mary))))
; John and Mary's mother

(mother (shift c (and (c 'john) (c 'mary))))
; John's mother and Mary's mother

Do continuations help us understand/reason about order of evaluation per se, or do they help us reason about order of evaluation in the context of a compositional semantics?

The latter, and thus the former, no? :)

In general, should the monad/continuation approach give us insights into natural language meaning (empirically relevant insights), or should it give us insights into how to analyze natural language meaning in a certain way, compositional semantics?

The latter, and thus the former, no? :) :)

It seems to me that the analogy between computational side effects and “apparently noncompositional” linguistic phenomena could be insightful in the first way, and that these insights would be conceptually prior to any implementation in terms of monads/continuations.

Sure, if I were patenting all this then I would claim an implementation in terms of monads/continuations as “a preferred embodiment” of the analogy.

Take weak crossover. The insight is that evaluation order matters. You and Ken used continuations to capture this compositionally. But now your account of order-sensitivity is order-independent. This is what we need for traditional, bottom-up compositional semantics. But why do we still want this? Or, what is the status of such a semantics? It is often said that a compositional semantics is necessary for humans to understand novel utterances. But I think it is apparent that weak crossover arises not because humans learn a compositional semantics which simulates order-sensitivity, but rather because of the actual order-sensitivity of processing (we hear from left to right). What kind of semantic system captures this directly?

You probably wouldn’t find any denotational account of evaluation order “direct” in your sense. The “kind of semantic system” you want is probably operational semantics. Indeed, the way I would argue that some denotational semantics accounts for evaluation order is to show that it corresponds to an operational semantics that obviously accounts for evaluation order.

Here’s another attempt to put things generally. Is natural language a language with side effects (e.g. C, OCaml), which really does work impurely/noncompositionally, but such that, at a level of abstraction, its behavior can be described compositionally? or is natural language a pure functional language (e.g. Haskell) which just happens to contain lexical items whose (pure functional) meanings simulate side effects?

If it is the former, which seems plausible, how does language “really” do what it does?

What’s the difference? In other words, what does “really” mean?

Haskell programs can perform IO and manipulate mutable state just fine. The “semantics/pragmatics interface” (aka “run-time system”) of Haskell lets you define a value “main”, of type “IO ()”, which gets performed when you eventually run the program. It’s like, how does a Hamblin set of alternatives get actually asked?

指數成長歌 The descriptive complexity of songs

In his paper ”The complexity of songs”, Knuth introduced the notion of the space complexity of a song and used it to account for music history. For example, compared to a song whose lyrics must be memorized verbatim, a song with a refrain has its space complexity reduced by a constant factor. To justify the quest for songs with reduced space complexity, Knuth appeals to cognitive science:

It is known [3] that almost all songs of length n require a text of length ~ n. But this puts a considerable space requirement on one’s memory, if many songs are to be learned; hence our ancient ancestors invented the concept of a refrain [14].

Knuth proceeds to give many examples of songs of differing space complexity, including ”m bottles of beer on the wall”, which has space complexity O(log n) because the song of m verses has length n = Θ(m log m) but can be defined in space O(log m). (The “log m” in ”m log m” is because it takes Θ(log m) words to name each m in English.)

There are actually two quantities that can be reasonably called the space complexity of a song. First, there is the length of the shortest program that generates the song, akin to Kolmogorov complexity. In cognitive-science terms, this is the amount of long-term memory needed to store the song for future recall. Second, there is the space required to generate the song, akin to the space complexity of an algorithm. In cognitive-science terms, this is the amount of short-term memory needed to perform the song. For many songs, the long-term and short-term space complexities coincide. This is the case for ”m bottles of beer on the wall”.

Which of the two notions did Knuth have in mind? On one hand, his citation ”[3]” above refers to Chaitin’s paper “On the length of programs for computing finite binary sequences: statistical considerations”. So, I would say long-term. On the other hand, after explaining how ”m bottles of beer on the wall” witnesses that there exist songs of complexity O(log n), Knuth failed to make the obvious further remark that “10^m−1 bottles of beer on the wall” witnesses that there exist songs of (long-term) complexity O(log log n)”. So, I would say short-term.

Below is another set of lyrics with long-term space complexity O(log log n) but short-term space complexity O(log n). I think its use of the A-not-A construction is more natural than restricting bottle counts to numbers of the form 10^m−1, but you may disagree. I’ll leave translation into English as an exercise.

這首歌
是指數成長
不是指數成長？

（指數～指數～～
　成長～成長～～喔～～
　指數～指數～～
　成長～成長～～喔～～）

你知道
這首歌
是指數成長
不是指數成長
不知道
這首歌
是指數成長
不是指數成長？

（指數～指數～～
　成長～成長～～喔～～
　指數～指數～～
　成長～成長～～喔～～）

我會問
你知道
這首歌
是指數成長
不是指數成長
不知道
這首歌
是指數成長
不是指數成長
不會問
你知道
這首歌
是指數成長
不是指數成長
不知道
這首歌
是指數成長
不是指數成長？

（指數～指數～～
　成長～成長～～喔～～
　指數～指數～～
　成長～成長～～喔～～）

他好奇
我會問
你知道
這首歌
是指數成長
不是指數成長
不知道
這首歌
是指數成長
不是指數成長
不會問
你知道
這首歌
是指數成長
不是指數成長
不知道
這首歌
是指數成長
不是指數成長
不好奇
我會問
你知道
這首歌
是指數成長
不是指數成長
不知道
這首歌
是指數成長
不是指數成長
不會問
你知道
這首歌
是指數成長
不是指數成長
不知道
這首歌
是指數成長
不是指數成長？

（指數～指數～～
　成長～成長～～喔～～
　指數～指數～～
　成長～成長～～喔～～）

Dependent equality

Thanks to Adam Chlipala for teaching me how to prove vec2list2vec. It means that converting a dependently typed vector to an ordinary list and back yields the same vector intact. But surely there is a simpler way?

Require Import List.

Require String.
Open Scope string_scope.
Ltac move_to_top x :=
  match reverse goal with
  | H : _ |- _ => try move x after H
  end.
Tactic Notation "assert_eq" ident(x) constr(v) :=
  let H := fresh in
  assert (x = v) as H by reflexivity;
  clear H.
Tactic Notation "Case_aux" ident(x) constr(name) :=
  first [
    set (x := name); move_to_top x
  | assert_eq x name; move_to_top x
  | fail 1 "because we are working on a different case" ].
Ltac Case name := Case_aux Case name.
Ltac SCase name := Case_aux SCase name.

Inductive vec (X: Type): nat -> Type :=
  | vnil: vec X 0
  | vcons: forall n: nat, X -> vec X n -> vec X (S n).

Implicit Arguments vnil [ [X] ].
Implicit Arguments vcons [ [X] [n] ].

Check (vcons 4 (vcons 2 (vcons 7 vnil))).

Fixpoint vec2list {X: Type} {n: nat} (v: vec X n): list X :=
  match v with
  | vnil => nil
  | vcons _ h t => cons h (vec2list t)
  end.

Fixpoint list2vec {X: Type} (l: list X): vec X (length l) :=
  match l with
  | nil => vnil
  | cons h t => vcons h (list2vec t)
  end.

Theorem vec2list_length: forall (X: Type) (n: nat) (v: vec X n),
  length (vec2list v) = n.
Proof.
  intros X n v. induction v as [| n' h t].
  Case "vnil". reflexivity.
  Case "vcons". simpl. rewrite -> IHt. reflexivity.
Qed.

Theorem list2vec2list: forall (X: Type) (l: list X),
  vec2list (list2vec l) = l.
Proof.
  intros X l. induction l as [| h t].
  Case "nil". reflexivity.
  Case "cons". simpl. rewrite -> IHt. reflexivity.
Qed.

Require Import Eqdep.
Lemma vec2list2vec': forall (X: Type) (l: list X) (n: nat) (v: vec X n),
  forall (EQ: length l = n), l = vec2list v ->
    v = match EQ in (_ = n) return vec _ n with
          | refl_equal => list2vec l
        end.
Proof.
  intros X l.
  induction l as [| h t]; simpl;
    intros n v EQ H; destruct v; inversion EQ as [EQ'].
  Case "nil". rewrite (UIP_refl _ _ EQ). reflexivity.
  Case "cons". inversion H. rewrite (IHt _ v EQ' H2). clear.
    generalize (list2vec t) EQ EQ'.
    rewrite EQ'. intros v EQ1 EQ2.
    rewrite (UIP_refl _ _ EQ1).
    rewrite (UIP_refl _ _ EQ2).
    reflexivity.
Qed.

Theorem vec2list2vec: forall (X: Type) (n: nat) (v: vec X n),
  v = match (vec2list_length X n v) in (_ = n) return vec _ n with
        | refl_equal => list2vec (vec2list v)
      end.
Proof.
  intros. apply vec2list2vec'. reflexivity.
Qed.

Grub default

Oh, to hell with all this screwy business with savedefault in Grub 2. Let’s just set the default in userspace.

---

$ cat /etc/rc.local 
#!/bin/sh -e
#
# rc.local
#
# This script is executed at the end of each multiuser runlevel.
# Make sure that the script will "exit 0" on success or any other
# value on error.
#
# In order to enable or disable this script just change the execution
# bits.
#
# By default this script does nothing.

/usr/bin/perl <<'END'
# Set grub default menu entry by inspecting /proc/cmdline and
# looking for its contents in /boot/grub/grub/cfg
# [ccshan 2010-06-21]
use strict;
my $cmdline;
{
    open my $fh, '<', '/proc/cmdline' or die $!;
    local $/;
    $cmdline = <$fh>;
    close $fh;
}
$cmdline =~ s/\A\s*BOOT_IMAGE=//;
$cmdline =~ s/\s+\z//;
open my $fh, '<', '/boot/grub/grub.cfg' or die $!;
my $title;
while (<$fh>)
{
    if (/^\s*menuentry\s+'([^']*)'/)
    { $title = $1 }
    elsif (defined $title and /^\s*linux\s+(.*\S)/ and $1 eq $cmdline)
    { exec "/usr/sbin/grub-set-default", $title }
}
close $fh;
print STDERR "Cannot find menu entry to set default\n";
END

exit 0

---

$ cat /etc/default/grub
# If you change this file, run 'update-grub' afterwards to update
# /boot/grub/grub.cfg.

GRUB_DEFAULT=saved
...

Implementing circularity using metaprogramming

Given a tree whose leaves are labeled by numbers, let us replace every label by the minimum label without traversing the tree twice.

type tree = Leaf of int | Branch of tree * tree;;

let repmin (t:tree) : tree =
  let present = ref max_int in
  let make = .!.<fun future -> .~(
    let rec process = function
      | Leaf x ->
          present := min x !present;
          .<Leaf future>.
      | Branch (t1,t2) ->
          .<Branch (.~(process t1), .~(process t2))>.
    in process t)>. in
  make !present;;

repmin (Branch (Branch (Leaf 1, Leaf 2), Leaf 3));;
(* Branch (Branch (Leaf 1, Leaf 1), Leaf 1) *)

Julia L. Lawall, 2001. Implementing circularity using partial evaluation. In Proceedings of PADO 2001: 2nd symposium on programs as data objects, ed. Olivier Danvy and Andrzej Filinski, 84–102. Lecture Notes in Computer Science 2053. (slides)