- Recent Changes 新聞
- History 歷史
- Preferences 喜好
 Discussion 討論
Discussion 討論
The first post in this series showed what walks are and how to walk right through a value. This second post will add walking down into and up out of a value. Again, you can download this post as a program.
{-# OPTIONS -W -fglasgow-exts #-} module WalkZip2 where import WalkZip1 import Data.Generics (Data) import Data.Char (isSpace)
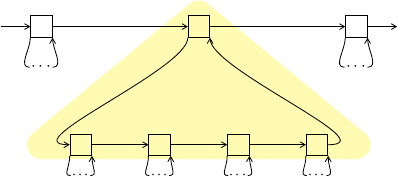
There are two ways to visualize a traversal.

The local way is to show the incoming and outgoing
directions for a single step. So far we have just one incoming
direction, Before, and just one outgoing direction,
After.
The global way to visualize a traversal is to show how its steps connect parts of a whole. So far all we can do is to forge right.
To traverse a value with hierarchical structure, we want to descend from a parent part to visit its children, and to ascend from a child part to admire its parent. Therefore, locally speaking, we add one incoming direction and one outgoing direction.
This way we connect a parent with its children as shown in the following global picture. In the top row are the parent and its siblings. In the bottom row are the children. The ellipses indicate the children’s cousins and own children.
The first time we visit a parent, we come in from its left. We can choose to skip the children by moving right or to visit the children by moving down. If we choose the latter, then after visiting all the children, we return to the parent from below, and can choose to move right or descend again. This loop is shaded in the global picture above.
As the local picture above shows, we rename the old directions
as we add the new directions. Each incoming direction
from—there is only one so far, namely
Before—becomes two incoming directions, Exit
False from and Exit True from. The latter
direction means that we just emerged from visiting the last child
in a horizontal sequence.
data Exit from = Exit Bool from deriving (Eq, Ord, Read, Show)
Each outgoing direction to—there is only one so
far, namely After—becomes an outgoing direction
To to alongside the new outgoing direction
Enter, which means to descend to the first child of
the current part.
data Enter to = Enter | To to deriving (Eq, Ord, Read, Show)
Every time a visitor arrives at a part, the walk orients the
visitor by passing an incoming direction. Every time a visitor
departs from a part, the visitor directs the walk by returning an
outgoing direction. In particular, if the visitor says to go down
(Enter) but there is no child to visit, the walk stays
at the same location and tells the visitor that there is no child
to visit by passing the incoming direction Exit True
Before. Indeed, as the last picture indicates, the way to go
up is to keep going right until you arrive at a part from
below.
That’s the plan. Let’s code it up. First we lift the incoming
direction before from any type from to
the type Exit from.
instance (From from) => From (Exit from) where before = Exit False before
We also lift the outgoing direction after from any
type to to the type Enter to.
instance (To to) => To (Enter to) where after = To after
To conduct recursive tourism, we define next to
descend once into everything. That is, descend when we arrive at a
part from the left, but continue to the right when we arrive at a
part from below.
instance (Next Before to) => Next (Exit Before) (Enter to) where next (Exit False Before) = Enter next (Exit True Before) = To after
We now build a walk combinator around, of the
following type.
around :: Walk from to part whole -> Walk (Exit from) (Enter to) part part -> Walk (Exit from) (Enter to) part whole
This combinator takes two walks walkOuter and
walkInner as argument and produces a new walk. In the
last picture, the top row corresponds to walkOuter and
the bottom row corresponds to walkInner. Whereas
walkOuter steps through parts of a whole,
walkInner steps through (sub)parts of a part. The new
walk is like walkOuter, except at any step the visitor
can Enter an inner walk to inspect the current
part.
The code for around is straightforward. The boring
part is how it uses the helper functions scavenge
(from last time) and pollute (below) to do the
dirty work of preserving sharing. The interesting part
is how it builds a visitor visit' for the outer walk
by wrapping around an inner walk that uses the original visitor
visit.
around walkOuter walkInner visit = walkOuter (visit' False False) where visit' dirty around from part = do (part1_, to) <- visit (Exit around from) part let (dirty1, part1) = pollute dirty part part1_ case to of Enter -> do part2_ <- walkInner visit part1 let (dirty2, part2) = pollute dirty1 part1 part2_ visit' dirty2 True from part2 To to -> return (scavenge dirty1 part1, to) pollute :: Bool -> a -> Maybe a -> (Bool, a) pollute dirty a Nothing = (dirty, a) pollute _ _ (Just a) = (True, a)
To try this out, let me first define a New York walk. A New York
walk makes no stops, not even
one.
newYork :: Walk from to part whole newYork _ _ = return Nothing
The New York walk is so brisk, no tourist gets to see anything or touch any button.
*WalkZip2> (newYork :: Walk Before After Term Term) tourist term Nothing *WalkZip2> (newYork :: Walk Before After Term Term) tourist' term Nothing
If we use the New York walk as the inner walk in
around, then no part has any subpart, so a visitor who
tries to enter a part is whisked right out.
*WalkZip2> (stop Before `around` newYork) tourist term Exit False Before: A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x"))) Exit True Before: A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x"))) Nothing
But if we put this walk in an inner walk, then a part can have subparts, though a subpart cannot have subsubparts, so a visitor who tries to enter a subpart is whisked out.
*WalkZip2> (stop Before `around` gwalk (stop Before `around` newYork)) tourist term Exit False Before: A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x"))) Exit False Before: L "x" (A (V "x") (V "x")) Exit True Before: L "x" (A (V "x") (V "x")) Exit False Before: L "x" (A (V "x") (V "x")) Exit True Before: L "x" (A (V "x") (V "x")) Exit True Before: A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x"))) Nothing
To go one level further into the term, we can put this last walk in an inner walk, so that only a subsubpart cannot have subsubsubparts.
*WalkZip2> (stop Before `around` gwalk (stop Before `around` gwalk (stop Before `around` newYork))) tourist term Exit False Before: A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x"))) Exit False Before: L "x" (A (V "x") (V "x")) Exit False Before: A (V "x") (V "x") Exit True Before: A (V "x") (V "x") Exit True Before: L "x" (A (V "x") (V "x")) Exit False Before: L "x" (A (V "x") (V "x")) Exit False Before: A (V "x") (V "x") Exit True Before: A (V "x") (V "x") Exit True Before: L "x" (A (V "x") (V "x")) Exit True Before: A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x"))) Nothing
To walk through all nodes of a tree, we take the fixpoint of this process.
throughout :: (Data a) => Walk from to a a -> Walk (Exit from) (Enter to) a a throughout level = level `around` gwalk (throughout level)
*WalkZip2> throughout (stop Before) tourist term Exit False Before: A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x"))) Exit False Before: L "x" (A (V "x") (V "x")) Exit False Before: A (V "x") (V "x") Exit False Before: V "x" Exit True Before: V "x" Exit False Before: V "x" Exit True Before: V "x" Exit True Before: A (V "x") (V "x") Exit True Before: L "x" (A (V "x") (V "x")) Exit False Before: L "x" (A (V "x") (V "x")) Exit False Before: A (V "x") (V "x") Exit False Before: V "x" Exit True Before: V "x" Exit False Before: V "x" Exit True Before: V "x" Exit True Before: A (V "x") (V "x") Exit True Before: L "x" (A (V "x") (V "x")) Exit True Before: A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x"))) Nothing
You might be tired of all this recursive tourism where the
visitor just follows a predetermined route and makes no
choice. I certainly much prefer interactive decision-making over
horseback flower-watching! To finish up this post, let’s control a
walk from the keyboard. The following visitor is convenient for
that: it prompts us at each step for what to return. A blank line
means to take the next step without making any
changes.
keyboard :: (Next from to, Show a, Read a) => from -> a -> IO (Maybe a, to) keyboard from x = do putStr (show from ++ ": " ++ show x ++ "\n? ") line <- getLine return (if all isSpace line then (Nothing, next from) else read line)
Let’s stroll through the term (λx.xx)(λx.xx) and change its second part to (λx.x), then double back to review the new term (λx.xx)(λx.x).
*WalkZip2> throughout (stop Before) keyboard term Exit False Before: A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x"))) ? Exit False Before: L "x" (A (V "x") (V "x")) ? (Nothing, To After) Exit False Before: L "x" (A (V "x") (V "x")) ? Exit False Before: A (V "x") (V "x") ? (Just (V "x"), Enter) Exit True Before: V "x" ? Exit True Before: L "x" (V "x") ? Exit True Before: A (L "x" (A (V "x") (V "x"))) (L "x" (V "x")) ? (Nothing, Enter) Exit False Before: L "x" (A (V "x") (V "x")) ? Exit False Before: A (V "x") (V "x") ? (Nothing, To After) Exit True Before: L "x" (A (V "x") (V "x")) ? (Nothing, To After) Exit False Before: L "x" (V "x") ? (Nothing, To After) Exit True Before: A (L "x" (A (V "x") (V "x"))) (L "x" (V "x")) ? (Nothing, To After) Just (A (L "x" (A (V "x") (V "x"))) (L "x" (V "x")))
In the next post, we will take a walk outside the
IO monad, to make a zipper.