- Recent Changes 新聞
- History 歷史
- Preferences 喜好
 Discussion 討論
Discussion 討論
In two previous posts, we saw how to walk right, down, and up
through a hierarchical value. At each step of the walk, the visitor
may inspect the part of the value at the current location and
change it if desired. The visitor may operate in any monad, such as
IO, so the inspection may occur by printing to
standard output and the change may be directed from standard input.
This third and final post of the series shows how to walk
left. Again, you can download this post
as a program.
{-# OPTIONS -W -fglasgow-exts #-} module WalkZip3 where import WalkZip1 import WalkZip2 import Control.Monad (liftM) import Control.Monad.Trans (MonadTrans(lift)) import Control.Monad.Cont (ContT(ContT), runContT) import Control.Monad.Error (Error(noMsg), ErrorT(runErrorT), throwError) import Data.Maybe (isJust, fromMaybe) import Data.Generics (Data) import Text.Show.Functions ()
In this post, we focus on a particular monad: not
IO but what we call the Zipper monad. A
computation in the Zipper monad either finishes with a
value, or produces some output and awaits some input
interactively. The output is the current value of a part,
along with the incoming direction from which the walk arrived at
the part. The input is the outgoing direction to which the walk
should continue from the part, and optionally a new value for the
part.
data Zipper from to part a = Done a | Stop from part (Maybe part -> to -> Zipper from to part a) deriving Show instance Monad (Zipper from to part) where return = Done Done a >>= k = k a Stop from part c >>= k = Stop from part c' where c' part' to = c part' to >>= k
The Zipper monad is designed to be the reification
of a walk. That is, we can turn any walk over a value into a
Zipper computation without losing any information. As
you might expect, this reification amounts to an inversion of
control using the continuation monad transformer (ContT
in the monad
transformer library): we pass a special visitor to the walk
(visit below) that captures the continuation of the
visit into a Stop computation.
zipper :: Walk from to part whole -> whole -> Zipper from to part (Maybe whole) zipper walk whole = runContT (walk visit whole) return where visit from part = ContT (Stop from part . curry)
In short, a zipper is a suspended walk. To continue the example
at the end of the previous post in this
series, let us use this zipper function to walk
through term. Recall that term is
(λx.xx)(λx.xx). When we convert the walk to a Zipper
using zipper, we no longer need to direct the walk
right away. Instead, we get a value that we can use to continue the
walk at our leisure. Let’s call this value start.
start = zipper (throughout (stop Before)) term *WalkZip3> :type start start :: Zipper (Exit Before) (Enter After) Term (Maybe Term) *WalkZip3> start Stop (Exit False Before) (A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x")))) <function>
As the last line above shows, the suspended walk
start has arrived at the entirety of the
term from the left. To continue this walk, we define a
convenience function continue, which simply extracts
the continuation from a Zipper that is at a
Stop.
continue :: Zipper from to part whole -> Maybe part -> to -> Zipper from to part whole continue (Done _) = error "Zipper is done, not at a stop" continue (Stop _ _ c) = c
Taking advantage of the fact that GHCi always binds the variable
it to the last expression evaluated, we can conduct
the same walk as at the end of the previous
post.
*WalkZip3> continue start Nothing Enter Stop (Exit False Before) (L "x" (A (V "x") (V "x"))) <function> *WalkZip3> continue it Nothing (To After) Stop (Exit False Before) (L "x" (A (V "x") (V "x"))) <function> *WalkZip3> continue it Nothing Enter Stop (Exit False Before) (A (V "x") (V "x")) <function> *WalkZip3> continue it (Just (V "x")) Enter Stop (Exit True Before) (V "x") <function> *WalkZip3> continue it Nothing (To After) Stop (Exit True Before) (L "x" (V "x")) <function> *WalkZip3> continue it Nothing (To After) Stop (Exit True Before) (A (L "x" (A (V "x") (V "x"))) (L "x" (V "x"))) <function> *WalkZip3> continue it Nothing Enter Stop (Exit False Before) (L "x" (A (V "x") (V "x"))) <function> *WalkZip3> continue it Nothing Enter Stop (Exit False Before) (A (V "x") (V "x")) <function> *WalkZip3> continue it Nothing (To After) Stop (Exit True Before) (L "x" (A (V "x") (V "x"))) <function> *WalkZip3> continue it Nothing (To After) Stop (Exit False Before) (L "x" (V "x")) <function> *WalkZip3> continue it Nothing (To After) Stop (Exit True Before) (A (L "x" (A (V "x") (V "x"))) (L "x" (V "x"))) <function> *WalkZip3> continue it Nothing (To After) Done (Just (A (L "x" (A (V "x") (V "x"))) (L "x" (V "x"))))
(Exercise: write a convenience function for the special case of
continue that corresponds to entering a blank line at
the keyboard.)
What Zipper lets us do that we couldn’t do before
is to go off and do something else at any step. We can resume a
suspended walk as long as we keep a Zipper value
around to represent it. In fact, we can resume the same suspended
walk multiple times (or not at all), just as we can invoke any
other function multiple times (or not at all). For example, we can
continue from the same start in two
different ways, and switch to one way whenever we get tired of the
other. Such multiprocessing is one of the earliest
applications discovered for
continuations.
*WalkZip3> continue start (Just (A (V "y") (V "z"))) Enter Stop (Exit False Before) (V "y") <function> *WalkZip3> let saved = it *WalkZip3> continue start (Just (L "x" (V "x"))) Enter Stop (Exit False Before) (V "x") <function> *WalkZip3> let saved' = it *WalkZip3> continue saved Nothing (To After) Stop (Exit False Before) (V "z") <function> *WalkZip3> continue saved' Nothing (To After) Stop (Exit True Before) (L "x" (V "x")) <function> *WalkZip3> continue saved Nothing Enter Stop (Exit True Before) (V "y") <function>
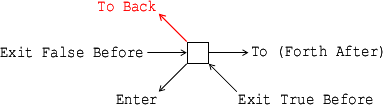
Reifying walks into zippers turns out to be the key to walking
to the left. Our goal in the rest of this post is to add
the red arrow “To Back” in the following local picture
of a walk—
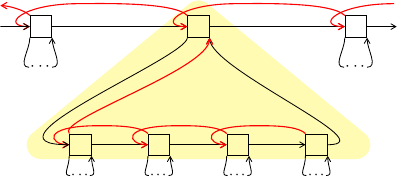
—or equivalently, to add the red arrows in the following global picture of a walk.
Intuitively, to walk left is to backtrack from walking right, so
a first approximation to walking left is to save up a bunch of
suspended walks—one for each previously encountered stop to the
left of our current location—and resume them in last-in-first-out
order as necessary. However, when we backtrack to the left, we need
to make sure not to lose any changes to the data that we might have
made on the right. To avoid losing the changes, we record them in a
data structure that we call Diff.
data Diff part to = Diff (Maybe part) to (Diff part to)
A Diff value is a serial record of a visitor’s
behavior over the course of a walk. It is best to think of the
definition of Diff above as an infinite list of pairs,
each a move by the visitor. The first component, of type
Maybe part, is an optional new part. The second
component, of type to, is an outgoing direction. If we
draw this infinite list as a tree, then to move from the list to a
suffix of it is to go down the tree.
Even though a Diff is an infinite data structure,
it is convenient to be able to show it. We show just the top 3
levels.
instance (Show part, Show to) => Show (Diff part to) where showsPrec = loop 3 where loop 0 _ _ = showString "..." loop l d (Diff part to diff) = showParen (d > 0) $ showString "Diff " . showsPrec 11 part . showChar ' ' . showsPrec 11 to . showString " $ " . loop (l - 1) 0 diff
An empty (initial) Diff record is a visitor that
keeps moving to the right without making any changes.
same :: (To to) => Diff part to same = Diff Nothing after same *WalkZip3> same :: Diff part After Diff Nothing After $ Diff Nothing After $ Diff Nothing After $ ... *WalkZip3> same :: Diff part (Enter After) Diff Nothing (To After) $ Diff Nothing (To After) $ Diff Nothing (To After) $ ...
Given a Zipper, we can replay any Diff
against it: just pass successive records in the Diff
to successive continuations offered by the Zipper,
until the Zipper is Done.
replay :: Zipper from to part whole -> Diff part to -> whole replay (Done whole) _ = whole replay (Stop _ _ c) (Diff part to diff) = replay (c part to) diff
For example, we can replay the Diff called
same against the Zipper called
start. Not surprisingly, such a replay yields no
changes to the term.
*WalkZip3> replay start same Nothing
Other Diffs are more exciting to replay. We can
replace the entire term, for instance.
*WalkZip3> replay start (Diff (Just (V "v")) (To After) same) Just (V "v")
Or we can replace just the first subterm.
*WalkZip3> replay start (Diff Nothing Enter $ Diff (Just (V "v")) (To After) $ same) Just (A (V "v") (L "x" (A (V "x") (V "x"))))
In fact, we can do much better: given a Zipper, we
can not only replay a Diff passively, but more
generally walk through a Diff actively. That
is, we can change a Diff while replaying it
against a Zipper. After all, a Diff is
just a tree structure, whose parts are its suffixes when regarded
as a list of moves. Therefore, we can walk through a
Diff in the directions we have already built: walking
down means to move into the future, whereas walking right or up
means to move into the past. If the visitor to the
Diff changes it during the walk, then we simply replay
the new Diff in place of the old one. The
walkDiff function below converts a zipper into such a
walk.
walkDiff :: (To to) => Zipper from to part whole -> Walk (Exit (Zipper from to part whole)) (Enter After) (Diff part to) (Diff part to) walkDiff zipper = stop zipper `around` \visit ~(Diff part to diff) -> case zipper of Done _ -> return Nothing Stop _ _ c -> liftM (liftM (Diff part to)) (walkDiff (c part to) visit diff)
In this walk, the type of incoming directions is that of a
Zipper. This way, every time we stop at a
Diff, the visitor can use information about the
current location to decide what to do. To replay the
Diff, we pass its part and
to components to the continuation c in
the Zipper (on the last line in the code above).
To recap, we can reify any walk into a zipper, and we can
convert any zipper into a walk over a Diff. To try
this out, let’s convert start into a walk over
same, then reify this walk into a zipper.
*WalkZip3> zipper (walkDiff start) same Stop (Exit False (Stop (Exit False Before) (A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x")))) <function>)) (Diff Nothing (To After) $ Diff Nothing (To After) $ Diff Nothing (To After) $ ...) <function>
All this nesting looks scary, but it merely repeats what we put
in: the first half of the output above is start, and
the second half is same. We can now replay
same against start step by step
and meddle in it as we please, as in a debugger. If we are happy
with the current Diff, namely same, we
can take one step forward in the replay. To step forward in the
replay is to go down (that is, Enter) the
Diff.
*WalkZip3> continue (zipper (walkDiff start) same) Nothing Enter Stop (Exit False (Done Nothing)) (Diff Nothing (To After) $ Diff Nothing (To After) $ Diff Nothing (To After) $ ...) <function>
The first line in the output above shows that the replay has
completed. The result is Nothing, just as when we
evaluated replay start same above. If that’s not
exciting enough, we can edit the Diff before stepping
forward. For example, let us edit the Diff so that it
starts by entering the term rather than going right through it.
*WalkZip3> continue (zipper (walkDiff start) same) (Just (Diff Nothing Enter same)) Enter Stop (Exit False (Stop (Exit False Before) (L "x" (A (V "x") (V "x"))) <function>)) (Diff Nothing (To After) $ Diff Nothing (To After) $ Diff Nothing (To After) $ ...) <function>
In the output above, the first half is the Zipper
after one step of replay, and the second half is the
Diff after one step of replay. Note that we are now at
the first subterm. We can take another step forward in the replay,
without editing the Diff this time, to move to the
second subterm.
*WalkZip3> continue it Nothing Enter Stop (Exit False (Stop (Exit False Before) (L "x" (A (V "x") (V "x"))) <function>)) (Diff Nothing (To After) $ Diff Nothing (To After) $ Diff Nothing (To After) $ ...) <function>
That looks like the same output, but we are now at the second
subterm. Let’s edit the Diff here to edit the
Term here.
*WalkZip3> continue it (Just (Diff (Just (V "v")) (To After) same)) Enter Stop (Exit False (Stop (Exit True Before) (A (L "x" (A (V "x") (V "x"))) (V "v")) <function>)) (Diff Nothing (To After) $ Diff Nothing (To After) $ Diff Nothing (To After) $ ...) <function>
In the first line of the output, Exit True Before
tells us that the Zipper has returned to the top level
of the term (by moving right from the second and last subterm). On
the second line is the new term, in which the second subterm of the
term has changed to V "v". If we like this new term,
there are two ways to finish up. First, if we just step forward
once more in the replay, then we reach the end of the replay and
recover the final term.
*WalkZip3> let changed = it *WalkZip3> continue changed Nothing Enter Stop (Exit False (Done (Just (A (L "x" (A (V "x") (V "x"))) (V "v"))))) (Diff Nothing (To After) $ Diff Nothing (To After) $ Diff Nothing (To After) $ ...) <function>
The rest of the infinite number of moves in same
remain unused as shown by the second component of Stop
above. Second, if we keep stepping back in the replay—by
stepping up (or equivalently, right) in the walk
over our Diff—then we gradually undo our changes to
the term but retain them in the changes to the Diff.
Watch the Diffs returned below as we build an
increasingly non-same list of moves.
*WalkZip3> continue changed Nothing (To After) Stop (Exit True (Stop (Exit False Before) (L "x" (A (V "x") (V "x"))) <function>)) (Diff (Just (V "v")) (To After) $ Diff Nothing (To After) $ Diff Nothing (To After) $ ...) <function> *WalkZip3> continue it Nothing (To After) Stop (Exit True (Stop (Exit False Before) (L "x" (A (V "x") (V "x"))) <function>)) (Diff Nothing (To After) $ Diff (Just (V "v")) (To After) $ Diff Nothing (To After) $ ...) <function> *WalkZip3> continue it Nothing (To After) Stop (Exit True (Stop (Exit False Before) (A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x")))) <function>)) (Diff Nothing Enter $ Diff Nothing (To After) $ Diff (Just (V "v")) (To After) $ ...) <function> *WalkZip3> continue it Nothing (To After) Done (Just (Diff Nothing Enter $ Diff Nothing (To After) $ Diff (Just (V "v")) (To After) $ ...))
Finally—on the last three lines above—we get an updated
Diff containing the history of all the changes we made
to the term. At any point above, we could have switched from
stepping back in the replay to stepping forward again (in other
words, switched from stepping out of the Diff to
stepping in again), and our recorded changes would have been
reinstated. This reinstatement of a historical record of changes is
what we need to walk left without losing changes to the right.
We are in the home stretch now. All that’s left to do is to
package up the insights demonstrated interactively above into a
function that adds a Back direction to any traversal.
Let’s define a new data type of outgoing directions.
data BackForth to = Back | Forth to deriving (Eq, Ord, Read, Show) instance (To to) => To (BackForth to) where after = Forth after instance (Next from to) => Next from (BackForth to) where next = Forth . next
Now we are ready for the backForth function, which
turns any walk with outgoing direction type to into a
walk with outgoing direction type BackForth to. In
other words, backForth adds a new outgoing direction
(namely Back) to any walk.
backForth :: (To to) => Walk from to part whole -> Walk from (BackForth to) part whole backForth walk visit whole = liftM (either id (>>= replay za)) (runErrorT (walkDiff za visit' same)) where za = zipper walk whole visit' (Exit _ (Done whole)) _ = throwError whole visit' (Exit _ (Stop from part _)) (Diff partD toD diffD) = do (part, to) <- lift (visit from (fromMaybe part partD)) let diff' | isJust part = Just (Diff part toD diffD) | otherwise = Nothing return (case to of Back -> (diff', after) Forth to -> (if to == toD then diff' else Just (Diff part to same), Enter))
The main body of this definition (liftM (...)
(...)) deals with the two ways in which a walk returned by
backForth may terminate. They correspond to the two
ways to “finish up” discussed above.
-
The first way is to reach the end of the replay, which means that we have walked off the right edge of the
whole. In that case, we are deep inside a traversal over aDiff, so we stop that traversal promptly by throwing an exception usingthrowErrorin the sum monad transformer (ErrorTin the monad transformer library). -
The second way is to reach the beginning of the reply, which means that we have walked off the left edge of the
whole. In that case, we have an updatedDiffand simplyreplayit against the originalwhole.
The rest of the code, in particular the auxiliary definition of
visit', converts a visitor to the whole
that may ask to go either Back or Forth
into a visitor to the Diff that may ask to go either
up or down.
To support our use of the sum monad transformer, because
Haskell’s Monad class includes the extra member
error, we need to define how to make an error value of
type Maybe whole. We don’t actually use this
definition.
instance Error (Maybe whole) where noMsg = Nothing
It’s time to put it all together. Recall from the first post that gwalk (stop
Before) is a walk that traverses the immediate parts of a
whole by moving right at every step. For demonstration, let’s
define walkTerm to be the special case where the parts
and the whole are both λ-terms.
walkTerm :: Walk Before After Term Term walkTerm = gwalk (stop Before) *WalkZip3> walkTerm keyboard term Before: L "x" (A (V "x") (V "x")) ? (Just (V "y"), After) Before: L "x" (A (V "x") (V "x")) ? Just (A (V "y") (L "x" (A (V "x") (V "x"))))
Applying backForth to walkTerm enables
it to move left as well as right.
*WalkZip3> backForth walkTerm keyboard term Before: L "x" (A (V "x") (V "x")) ? (Just (V "y"), Forth After) Before: L "x" (A (V "x") (V "x")) ? (Just (V "z"), Back) Before: V "y" ? Before: V "z" ? Just (A (V "y") (V "z"))
Applying throughout to backForth
walkTerm enables it to move up and down as well as left and
right.
*WalkZip3> throughout (backForth walkTerm) keyboard term Exit False Before: L "x" (A (V "x") (V "x")) ? Exit False Before: V "x" ? Exit True Before: V "x" ? Exit False Before: V "x" ? (Just (V "y"), To Back) Exit False Before: V "x" ? (Nothing, To (Forth After)) Exit False Before: V "y" ? (Nothing, To (Forth After)) Exit True Before: L "x" (A (V "x") (V "y")) ? (Nothing, To (Forth After)) Exit False Before: L "x" (A (V "x") (V "x")) ? (Nothing, To (Forth After)) Just (A (L "x" (A (V "x") (V "y"))) (L "x" (A (V "x") (V "x"))))
Generalizing this development, we define a generic function to walk through any data structure in all four directions.
through :: (Data a) => Walk (Exit Before) (Enter (BackForth After)) a a through = stop' `around` throughout (backForth (gwalk stop')) where stop' visit = liftM fst . visit before
The final test below produces the same output as the previous test, except it starts and ends at the top level with the entire value.
*WalkZip3> through keyboard term Exit False Before: A (L "x" (A (V "x") (V "x"))) (L "x" (A (V "x") (V "x"))) ? Exit False Before: L "x" (A (V "x") (V "x")) ? Exit False Before: V "x" ? Exit True Before: V "x" ? Exit False Before: V "x" ? (Just (V "y"), To Back) Exit False Before: V "x" ? (Nothing, To (Forth After)) Exit False Before: V "y" ? (Nothing, To (Forth After)) Exit True Before: L "x" (A (V "x") (V "y")) ? (Nothing, To (Forth After)) Exit False Before: L "x" (A (V "x") (V "x")) ? (Nothing, To (Forth After)) Exit True Before: A (L "x" (A (V "x") (V "y"))) (L "x" (A (V "x") (V "x"))) ? Just (A (L "x" (A (V "x") (V "y"))) (L "x" (A (V "x") (V "x"))))
To conclude, this series of posts has presented a notion of traversal that is generic in the type of directions and the monad of visits. Starting with unrelenting forward movement, such traversals can be transformed in several ways:
- A fixpoint operation adds vertical movement.
- A reification operation turns a traversal into a zipper by inverting control.
- Traversing a historical record of changes, replayed against a zipper, adds backward movement.