In the last post in this series, we figured out:

If the integers from 1 to 999,999,999 are written as words in numerical order and concatenated, what is the 51 billionth letter?

The goal of this final post is to figure out:

If the integers from 1 to 999,999,999 are written as words in alphabetical order and concatenated, what is the 51 billionth letter?

For example, if we write the integers from 1 to 3 as words in alphabetical order and concatenate them, then we get “onethreetwo”, so the 51 billionth letter is… well, there is no 51 billionth letter.

Still we plunge ahead. As before, you can download this post as a program.

{-# OPTIONS -W -fglasgow-exts #-}
module WordNumbers4 where
import WordNumbers1
import WordNumbers2
import WordNumbers3 (volume)
import Prelude hiding ((+), (*), sum, product)
import qualified Data.Map as M

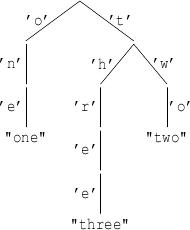
To put our 999,999,999 strings into alphabetical order, we use a most-significant-digit radix sort. That is, we group the strings by their first letter, then further divide each group of strings by their second letter, and so on. The result of this recursive grouping is a tree whose edges are each labeled by a letter and whose nodes are inhabited by strings. This tree is also called a trie.

At each node in this tree, the outgoing edges are sorted by their letter labels. Therefore, given the tree, we can recover a sorted list of strings by traverse it from left to right in prefix order. Of course, rather than traversing the tree, we actually want to descend into it by binary search. Hence, we build the tree lazily and record at each node not just the strings inhabiting that node but also the sum of the strings inhabiting all descendants of that node. Accordingly, we define the following data type.

data Trie c m = Trie { total :: m,
                       label :: m,
                       children :: M.Map c (Trie c m) }
  deriving (Eq, Show)

The type variable c above is the type of letters, and the type variable m is the type of node labels, so the children field of a Trie maps letters to tries. The total of a Trie should be the sum of the labels of all of its nodes; in other words, if t is a Trie then it should satisfy the invariant

total t == label t + sum (map total (M.elems (children t))).

Now we want Trie Char m to be an instance of Character and Seminearring whenever m is. It is easy to define the Character instance: the char method simply builds a stump for a tree.

instance (Monoid m, Character m)
  => Character (Trie Char m) where
  char c = Trie r zero (M.singleton c (Trie r r M.empty))
    where r = char c

To define the Seminearring instance for Trie, we first need to define the Monoid instance because Monoid is a superclass of Seminearring. The Monoid instance for Trie is easy to define given a Monoid instance for Map.

instance (Ord k, Monoid v) => Monoid (M.Map k v) where
  zero = M.empty
  (+) = M.unionWith (+)

instance (Ord c, Monoid m) => Monoid (Trie c m) where
  zero = Trie zero zero zero
  Trie t1 e1 r1 + Trie t2 e2 r2
    = Trie (t1 + t2) (e1 + e2) (r1 + r2)

The Seminearring instance for Trie is easy to define given a Module instance for Map. As a minor optimization, we check for the special case of scaling a map by zero: in that case, we return an empty map rather than a map full of zeroes.

instance (Ord k, Eq r, Seminearring r)
  => Module r (M.Map k r) where
  r *> m | r == zero = M.empty
         | otherwise = fmap (r *) m
  m <* r | r == zero = M.empty
         | otherwise = fmap (* r) m

The multiplication operation on tries is crucially not symmetric, like string concatenation.

instance (Ord c, Eq m, Seminearring m)
  => Seminearring (Trie c m) where
  one = Trie one one zero
  Trie t1 e1 r1 * r@(Trie t2 e2 r2)
    = Trie (t1 * t2) (e1 * e2) (r1 <* r + e1' *> r2)
    where e1' = Trie e1 e1 M.empty `asTypeOf` r

We test these instances using the integers from 1 to 3.

*WordNumbers4> strings "one two three" :: Trie Char [String]
Trie {total = ["one","two","three"], label = [], children = fromList
[('o',Trie {total = ["one"], label = [], children = fromList
      [('n',Trie {total = ["one"], label = [], children = fromList
            [('e',Trie {total = ["one"], label = ["one"], children = fromList []})]})]}),
 ('t',Trie {total = ["two","three"], label = [], children = fromList
      [('h',Trie {total = ["three"], label = [], children = fromList
            [('r',Trie {total = ["three"], label = [], children = fromList
                  [('e',Trie {total = ["three"], label = [], children = fromList
                        [('e',Trie {total = ["three"], label = ["three"], children = fromList []})]})]})]}),
       ('w',Trie {total = ["two"], label = [], children = fromList
            [('o',Trie {total = ["two"], label = ["two"], children = fromList []})]})]})]}

We could also generate node labels of type Count or of type Deriv Count Volume, by replacing the type [String] in the expression above.

Let us now implement binary search over the trie. We keep a running tally of the node label skipped over so far, and compare the tally to the target using a callback function. The search returns two results: (1) the sequence of edge labels on the path from the root node to the target node; (2) the sum of the labels of all nodes to the left of the target node (inclusive). These two results correspond to the two accumulating arguments of the helper functions searchTrie and searchMap, defined locally below.

search :: (Monoid m) => (m -> Bool) -> Trie Char m -> (String, m)
search stop = searchTrie [] zero where
  searchTrie cs m t
    | stop m'   = (reverse cs, m')
    | otherwise = searchMap cs m' (M.assocs (children t))
    where m' = m + label t
  searchMap cs m ((c,t):cts)
    | stop m'   = searchTrie (c:cs) m t
    | otherwise = searchMap cs m' cts
    where m' = m + total t
  searchMap _ _ [] = error "Fell off the end of a child list"

The types Char and String above could be generalized to c and [c], but we give search the more specific type to avoid some type signatures below.

(Brandon Michael Moore’s solution to the puzzle inspires the following exercise: revise search to return a zipper at the target location rather than an ordered pair, so that the user of search can easily acquire any information desired near the target location.)

Using this binary search, we can find the first string in the sorted list…

*WordNumbers4> search (>= Nat 1) ten9
("eight",1)

… as easily as the last string or the middle one.

*WordNumbers4> search (>= Nat 999999999) ten9
("twothousandtwohundredtwo",999999999)
*WordNumbers4> search (>= Nat 500000000) ten9
("onehundredonemilliononehundredseventhousandtwohundredtwentyone",500000000)

In these searches, ten9 takes the type Trie Char Count. To query the trie by counting strings rather than characters, we use ten9 at the type Trie Char (Deriv Count Volume).

*WordNumbers4> search ((>= 51000000000) . volume) ten9
("sixhundredseventysixmillionsevenhundredfortysixthousandfivehundredseventyfive",Deriv 723302492 51000000000)

The number 51000000000 at the end of the output above confirms ITA Software’s assertion that

The 51 billionth letter also completes the spelling of an integer.

But wait, we’re not done yet! The original problem statement goes on to ask:

Which one, and what is the sum of all the integers to that point?

We have only answered the first half of this question. To answer the second half, we need to keep track of not just the count (number of strings) and volume (number of characters) of a set of strings but also the sum of a set of integers at the same time. We call this sum the mass. Luckily for us, the mass is a derivative just as the volume is: we can treat the list of strings

["one","two","three","four","five",...]

as a polynomial in two variables x and y, whose first few terms are

x³y¹ + x³y² + x⁵y³ + x⁴y⁴ + x⁴y⁵ + …

As before, if we evaluate this polynomial at x = y = 1, we get the count. Also as before, if we evaluate its derivative with respect to x at x = y = 1, we get the volume. What’s new is that, if we evaluate its derivative with respect to y at x = y = 1, we get the mass!

To solve ITA’s puzzle in full, then, we use the seminearring Measure defined as follows.

data M
type Mass = Wrap M (Nat Integer)
type Measure = Deriv Count (Volume, Mass)

To keep track of two derivatives (volume and mass) at the same time, we need to write a boring Module instance for pairs.

instance (Module r a, Module r b) => Module r (a,b) where
  r *> (a,b) = (r *> a, r *> b)
  (a,b) <* r = (a <* r, b <* r)

The main remaining question is, where does mass come from? A letter by itself has count 1 and volume 1…

*WordNumbers4> char undefined :: Count
1
*WordNumbers4> char undefined :: Volume
1

… but no mass.

instance Character Mass where
  char _ = zero

*WordNumbers4> char undefined :: Mass
0

After all, nothing in our grammar ten9 indicates the numeric values of the strings. Nothing, that is, except the order of the strings: recall that ten9 lists strings in numeric order.

*WordNumbers4> take 5 ten9 :: [String]
["one","two","three","four","five"]

What we need to do, then, is to define a new seminearring that is like Trie Char Measure except it automatically assigns the first string in the list the mass 0, the second string the mass 1, the third string the mass 2, and so on. Let us call this seminearring Numbered Char.

newtype Numbered c = Numbered (Trie c Measure)

instance Character (Numbered Char) where
  char = Numbered . char

The wrapper type Numbered lets us automate the assignment of masses to a list of strings, in two steps. First, when adding two lists of strings together, the mass of each string in the second list increases by the number of strings in the first list. This increase is because the string that used to be at index m in the second list is now at index n + m in the combined list, where n is the number of strings in the first list. (More generally, a bunch of c strings that used to have total mass m in the second list now have total mass cn + m in the combined list.)

instance (Ord c) => Monoid (Numbered c) where
  zero = Numbered zero
  Numbered a + Numbered b = Numbered (a + fmap f b)
    where Deriv n _ = total a
          f (Deriv c (v,m)) = Deriv c (v, Wrap (c * n) + m)

Second, when multiplying two lists of strings together, the mass of each string in the first list is scaled by the number of strings in the second list. This scaling is because the string that used to be at index m in the first list now begins index mn in the combined list, where n is the number of strings in the second list.

instance (Ord c) => Seminearring (Numbered c) where
  one = Numbered one
  Numbered a * Numbered b = Numbered (fmap f a * b)
    where Deriv n _ = total b
          f (Deriv c (v,m)) = Deriv c (v, m <* n)

These two instance definitions use the fact that Trie is a Functor.

instance Functor (Trie c) where
  fmap f (Trie t e r) = Trie (f t) (f e) (fmap (fmap f) r)

Done! Because our list of strings begins at “one” rather than “zero”, we prepend an empty string (“one +”) to correct the masses.

answer | target == volume m = (string, mass m)
       | otherwise = error "The target letter does not end a string"
  where target = 51000000000
        Numbered grammar = one + ten9
        (string, m) = search stop grammar
        stop m = volume m >= target
        volume (Deriv _ (Wrap (Nat n), _)) = n
        mass   (Deriv _ (_, Wrap (Nat n))) = n

The answer to the puzzle is an ordered pair.

*WordNumbers4> answer
("sixhundredseventysixmillionsevenhundredfortysixthousandfivehundredseventyfive",413540008163475743)

Update: Fixed the trie invariant along with some problems in grammar and indentation.